Secret Handshakes
Einleitung
Secret Handshakes ermöglichen es die Mitgliedschaft in einer Gruppe zu authentifizieren und gleichzeitig die eigene Anonymität im Falle des Misserfolgs sicherzustellen. In der Praxis stellen sie eine Erweiterung des SSL- bzw. TLS-Handshakes dar, der lediglich dazu dient einen Session Key für eine gesicherte Kommunikation auszuhandlen.
Secret Handshakes sollen ein geeignetes Mittel darstellen um Anonymität im Netzwerk/Internet sicherzustellen und die Privatsphäre von Personen und Institutionen zu schützen. Schon im üblichen Client-Server-Szenario können sie Anwendung finden um z.B. den Inhalt von Webservern vor Fremden zu verstecken und nur berechtigten Klienten Zutritt zu verschaffen.
Mathemathische Grundlagen
Um die nachfolgende Funktionsweise eines Secret Handshakes besser zu verstehen, gehen wir zunächst kurz auf die verwendeten mathematischen Konstrukte ein.
Gruppen
Eine Gruppe G(M, *) besteht aus einer Menge M und einer Verknüpfung *. Weiterhin ist in der Menge M das neutrale Element der Gruppe G enthalten. Ein Gruppe besitzt ein inverses Element. Abschließend ist die Verknüpfung einer Gruppe assoziativ.
Bei Secret Handshakes werden allerdings zyklische Gruppen verwendet.
zyklische Gruppen
Eine endliche zyklische Gruppe G(M, *) heißt zyklisch, wenn die Menge M mindestens ein Element g mit der Eigenschaft M = {g¹, g², g³, ... , g^n} enthält. Man nennt g dann erzeugendes Element der Gruppe. n stellt die Ordnung der Gruppe dar. Gruppen mit einer primen Ordnung q sind immer zyklisch.
bilineare Abbildungen
Ein weiteres wichtiges Thema zum Verständnis der Secret Handshakes sind bilineare Abbildungen.
Eine Abbildung f: E x F → G nennt man bilinear, wenn folgenes gilt:
- für festes x: Die Abbildung f(x, ·): F → G ist linear.
- für festes y: Die Abbildung f(·, y): E → G ist linear.
speziell benötigte lineare Abbildung
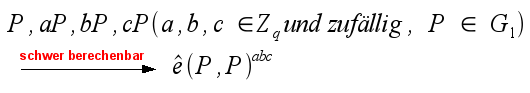
Bei den Secret Handshakes wird eine spezielle bilineare Abbildung ê: G_1 x G_1 → G_2 benötigt. Diese hat muss folgende Eigenschaften besitzen:
- G_1 und G_2 sind zyklische Gruppen mit der Primordnung q
- für alle a, b Element aus Z_q gilt: ê(aP, bQ) = ê(P, Q)^ab
Z_q soll hier für einen Restklassenring stehen.
Modifizierte Weil- und Tate-Paarungen über supersinguläre [elliptische Kurven] sind Beispiele für solche bilineare Abbildungen. Diese sind effizient berechenbar, nicht degenerativ und das bilineare Diffie-Hellman-Problem gilt für sie als schwer berechenbar.
Hashfunktionen
Für die Umsetzung der Secret Handshakes werden nun noch zwei Hashfunktionen benötigt.
erste Hashfunktion: H_1: {0,1}* → G_1
- Abbildung beliebiger Zeichenketten auf die zyklische Gruppe G_1
zweite Hashfunktion: H_2: {0,1}* → {0,1}*
- Abbildung beliebiger Zeichenketten auf Zeichenketten fester Länge
- kollisionsresistent
- z. B. SHA-1
Allgemeines Prinzip
[TODO]
Pairing Based Handshake Schema
[TODO]
Ablauf im Detail
Der gesamte Handshake besteht im wesentlichen aus 3 Schritten.
Am Anfang besteht (irgendwie) eine ungesicherte Verbindung zwischen den beiden, die den Handshake ausführen wollen.
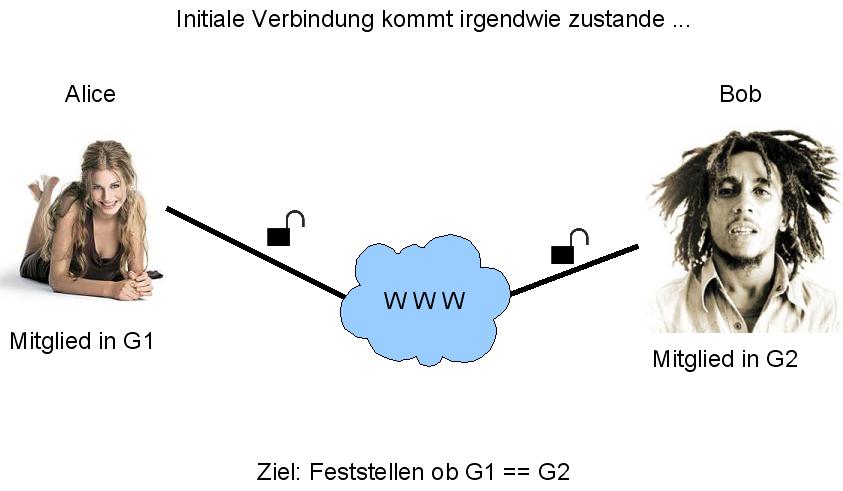
Alice beginnt nun indem sie eines ihrer Pseudonyme auswählt und dies zusammen mit einer zufälligen Zahl an Bob übermittelt.
Bob generiert nun seinerseits eine zufällige Zahl und berechnet zusammen mit einem seiner eigenen Secret Points die Zahl Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V_0 = H_2(ê(H_1(id_A), priv_B) parallel id_A parallel id_B parallel rand_A parallel rand_B parallel 0))}
.
Sicherheit gegen Abhören
[TODO]
Zusätzliche Eigenschaften
Vom vorgestellten Schema sind folgende Eigenschaften bereits umgesetzt: Forward Repudiability, Indistinguishability to Eavesdroppers, Unlinkability, Collusion Resistance und Traceability.
Forward Repudiability
Es ist trotz eines erfolgreichen Handshakes nicht möglich die Gruppenmitgliedschaft des anderen Teilnehmers nachzuweisen selbst wenn die eigenen Geheimnisse (die Secret Points) veröffentlicht werden. Der Grund dafür ist, dass ein Protokoll eines erfolgreichen Handshakes allein mit diesen Informationen generiert werden könnte, so dass dieses Protokoll keinen Beweis darstellen kann.
Indistinguishability to Eavesdroppers
Das Beobachten eines Handshakes gibt keinerlei Auskunft über die Gruppenmitgliedschaften der Beteiligten oder über den Erfolg des Handshakes. (Der Umstand weiter Kommunikation nach dem Handshakes könnte dies allerdings zunichte machen.)
Unlinkability
Die Nutzung von Listen von Pseudonymen für jeden einzelnen Nutzer macht es unmöglich, dass ein Beobachter anhand zweier (oder mehrerer) Handshakes feststellen kann, ob die gleichen Nutzer beteiligt waren. Listen von Pseudonymen erhöhen allerdings den Aufwand und könnten somit auf Grund von Performanceverbesserungen zu Lasten der Sicherheit aufgegeben werden. (Die Verwaltung von Revocation-Listen wird so wesentlich leichter.)
Collusion Resistance und Traceability
Selbst wenn eine Menge von Nutzern die eigenen Geheimnisse untereinander austauscht, bleibt das System sicher. Um das Gruppengeheimnis aus den Geheimnissen der Menge zu berechnen wäre es wiederum nötig das bilineare Diffie-Hellman-Problem zu lösen. (Collusion Resistance) Wenn andere Nutzer durch die Menge der konspirativen Nutzer korrumpiert werden, kann wenigestens einer aus dieser Menge festgestellt und anhand seiner benutzten Pseudonyme verfolgt werden. (Traitor tracing)
Rollen
Als weitere Eigenschaft sind verschiedene Rollen innerhalb der Gruppen vorstellbar. Dazu muss während der Authentifizierung nur das Pseudonym des Gegenübers mit der Rolle, die man von ihm erwartet, konkateniert werden. Der weitere Verlauf ist analog. Desweiteren sind nun natürlich alle Secret Points abhängig von Pseudonym und Rolle.
Anpassung des TLS Handshakes
[TODO]
Quellen
- Secret Handshakes from Pairing-Based Key Agreements (2003) Dirk Balfanz, Glenn Durfee, Narendar Shankar, Diana Smetters, Jessica Staddon, Hao-Chi Wong. [1]