Secret Sharing: Difference between revisions
No edit summary |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
=== Example === |
=== Example === |
||
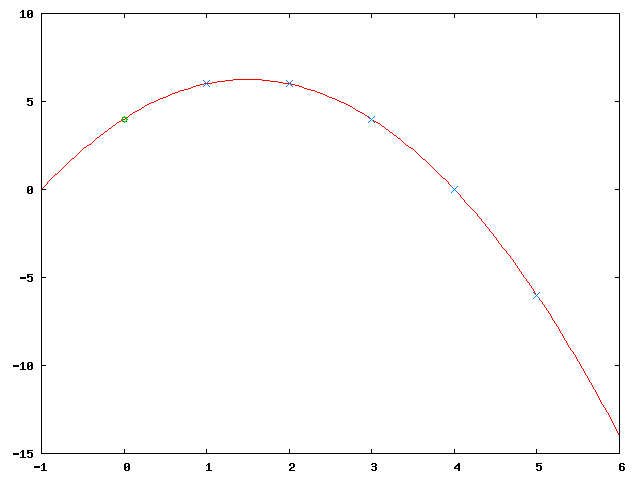
Let <math>D = 4</math>, <math>k = 3</math>, <math>n = 5</math>, that is: The secret is split into 5 parts of which at least 3 are necessary to reconstruct the secret. |
Let <math>D = 4</math>, <math>k = 3</math>, <math>n = 5</math>, that is: The secret is split into 5 parts of which at least 3 are necessary to reconstruct the secret. |
||
Now generate 2 random numbers <math>a_1</math> and <math>a_2</math>, let's say: <math>a_1 = 3</math>, <math>a_2 = -1</math> which give the polynomial <math>f(x) = 4 + 3 x - 1 x^2</math>. Obviously that's a quadratic function and any 3 points on the function are sufficient to interpolate the function. |
|||
[[Image:Secret-Sharing-polynomial.png]] |
|||
The image shows the resultant function (in red), the original secret (in green, at <math>x=0</math>) and the 5 new secret parts (in blue). |
|||
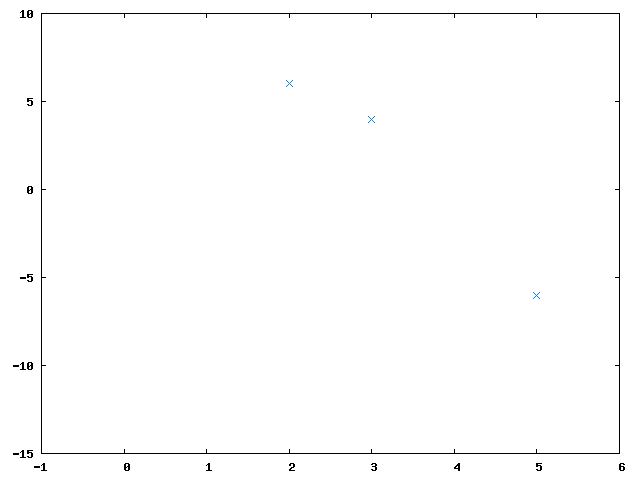
To reconstruct the original secret any 3 secret parts (let's say <math>D_2, D_3</math> and <math>D_5</math>) are merged together: |
|||
[[Image:Secret-Sharing-merging.png]] |
|||
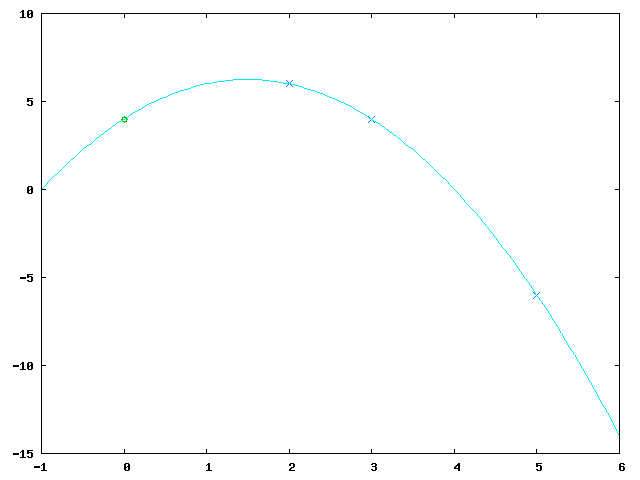
Then the polynomial is interpolated and <math>f(0)</math> computed: |
|||
[[Image:Secret-Sharing-reconstruction.png]] |
|||
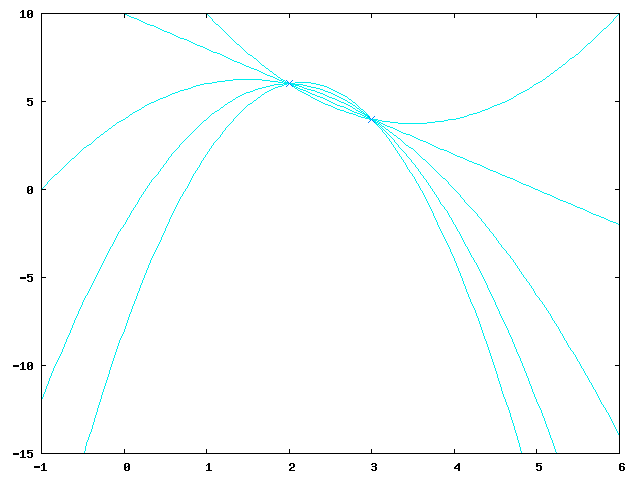
Let's suppose we wanted to reconstruct the shared secret but only had two of the parts: <math>D_2</math> and <math>D_3</math>. This gives two equations: |
|||
* <math>6 = a_0 + 2 a_1 + 4 a_2</math> |
|||
* <math>4 = a_0 + 3 a_1 + 9 a_2</math> |
|||
with three unknown variables thus allowing for infinitely many solutions which are all equally likely. |
|||
The image shows five of them (for <math>a_2 = -3</math>, <math>a_2 = -2</math>, <math>a_2 = -1</math>, <math>a_2 = 0</math> and <math>a_2 = 1</math>): |
|||
[[Image:Secret-Sharing-security.png]] |
|||
<table border="1" style="text-align: right"> |
|||
<tr><th><math>a_0</math></th><th><math>a_1</math></th><th><math>a_2</math></th></tr> |
|||
<tr><td>16</td><td>-7</td><td>1</td></tr> |
|||
<tr><td>10</td><td>-2</td><td>0</td></tr> |
|||
<tr><td>4</td><td>3</td><td>-1</td></tr> |
|||
<tr><td>-2</td><td>8</td><td>-2</td></tr> |
|||
<tr><td>-8</td><td>13</td><td>-3</td></tr> |
|||
</table> |
|||
Latest revision as of 13:15, 1 December 2004
Secret Sharing is used to split a secret (usually a key) into several pieces which are then given to distinct persons so that some of these persons must cooperate to reconstruct the secret.
A Simple Approach
One simple approach to split a secret number into pieces … such that any pieces are sufficient (and necessary) to reconstruct is using a polynomial.
When splitting the secret a random polynomial … with is generated. The are calculated as for ….
Given any it is possible to interpolate the polynomial and calculate which gives the original secret .
Example
Let , , , that is: The secret is split into 5 parts of which at least 3 are necessary to reconstruct the secret.
Now generate 2 random numbers and , let's say: , which give the polynomial . Obviously that's a quadratic function and any 3 points on the function are sufficient to interpolate the function.
The image shows the resultant function (in red), the original secret (in green, at ) and the 5 new secret parts (in blue).
To reconstruct the original secret any 3 secret parts (let's say and ) are merged together:
Then the polynomial is interpolated and computed:
Let's suppose we wanted to reconstruct the shared secret but only had two of the parts: and . This gives two equations:
with three unknown variables thus allowing for infinitely many solutions which are all equally likely.
The image shows five of them (for , , , and ):
| 16 | -7 | 1 |
| 10 | -2 | 0 |
| 4 | 3 | -1 |
| -2 | 8 | -2 |
| -8 | 13 | -3 |