Secret Sharing

Secret Sharing is used to split a secret (usually a key) into several pieces which are then given to distinct persons so that some of these persons must cooperate to reconstruct the secret.

A Simple Approach

One simple approach to split a secret number $D$ into $n$ pieces $D_{1}, D_{2},$ … $, D_{n}$ such that any $k$ pieces are sufficient (and necessary) to reconstruct $D$ is using a $k - 1$ polynomial.

When splitting the secret a random polynomial $f (x) = a_{0} + a_{1} x + a_{2} x +$ … $+ a_{k - 1} x^{k - 1}$ with $a_{0} = D$ is generated. The $D_{i}$ are calculated as $D_{i} = f (i)$ for $i = 1,$ … $, n$ .

Given any $k$ $D_{i}$ it is possible to interpolate the polynomial and calculate $f (0)$ which gives the original secret $D$ .

Example

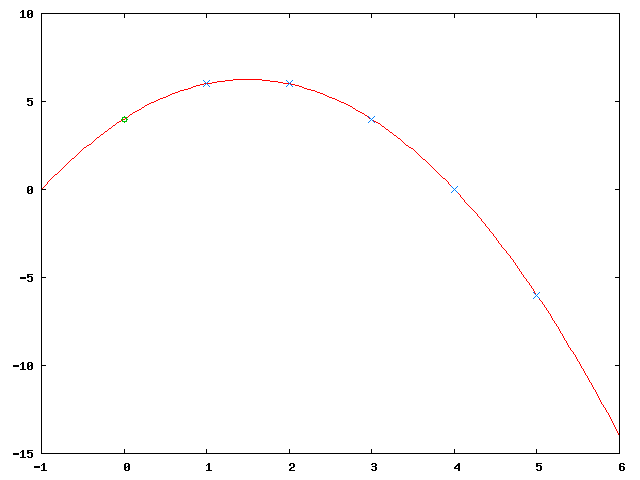
Let $D = 4$ , $k = 3$ , $n = 5$ , that is: The secret is split into 5 parts of which at least 3 are necessary to reconstruct the secret.

Now generate 2 random numbers $a_{1}$ and $a_{2}$ , let's say: $a_{1} = 3$ , $a_{2} = - 1$ which give the polynomial $f (x) = 4 + 3 x - 1 x^{2}$ . Obviously that's a quadratic function and any 3 points on the function are sufficient to interpolate the function.

The image shows the resultant function (in red), the original secret (in green, at $x = 0$ ) and the 5 new secret parts (in blue).

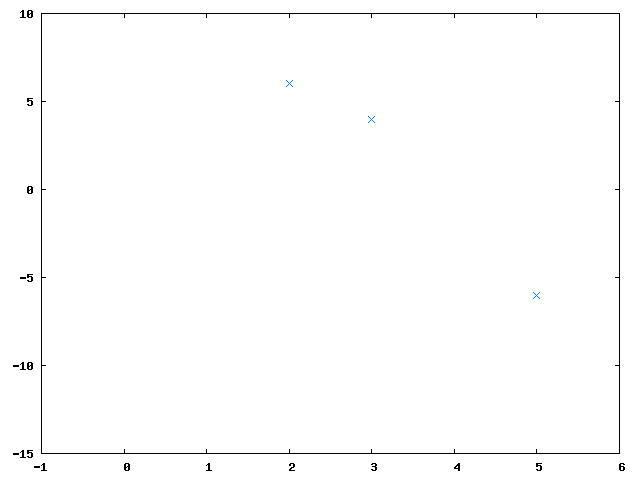
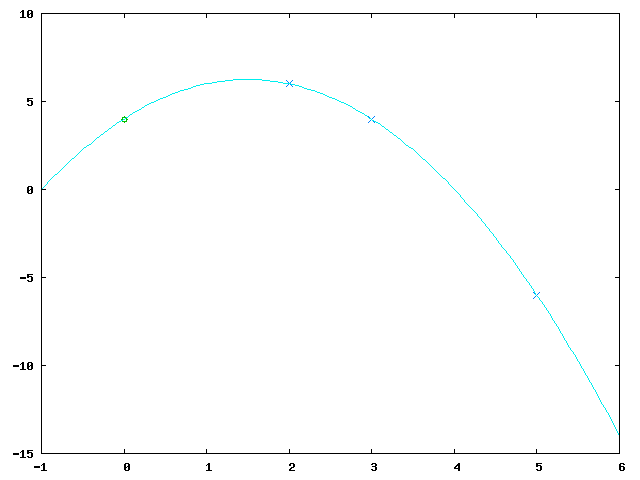
To reconstruct the original secret any 3 secret parts (let's say $D_{2}, D_{3}$ and $D_{5}$ ) are merged together:

Then the polynomial is interpolated and $f (0)$ computed:

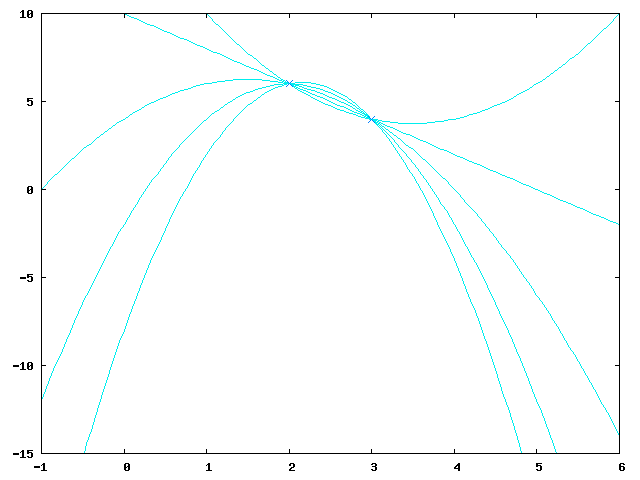
Let's suppose we wanted to reconstruct the shared secret but only had two of the parts: $D_{2}$ and $D_{3}$ . This gives two equations:

$6 = a_{0} + 2 a_{1} + 4 a_{2}$
$4 = a_{0} + 3 a_{1} + 9 a_{2}$

with three unknown variables thus allowing for infinitely many solutions which are all equally likely.

The image shows five of them (for $a_{2} = - 3$ , $a_{2} = - 2$ , $a_{2} = - 1$ , $a_{2} = 0$ and $a_{2} = 1$ ):

$a_{0}$	$a_{1}$	$a_{2}$
16	-7	1
10	-2	0
4	3	-1
-2	8	-2
-8	13	-3

Secret Sharing

A Simple Approach

Example

Navigation menu

Search