Maximum Battery Life Routing
Introduction
Most ad hoc mobile devices operate on batteries. The remaining battery capacity limits the lifetime of hosts and with that the possibility to send, receive or relay data. There is also an important influence on the overall communication performance and the lifetime of the ad hoc mobile wireless net, because the lack of hosts can result in partitioning of the network. So power consumption becomes an important issue.
Power conservation can be realized at different layers, e.g. at the physical layer/wireless device by using low-power hardware, by turning conventional components off or slowing them down when not needed and by adjusting of transmission power, further at the data link layer by using effective retransmission request schemes and sleep mode operation. In the following power-efficient routing algorithms at the network layer are the point of reflections.
Power-Efficient Routing
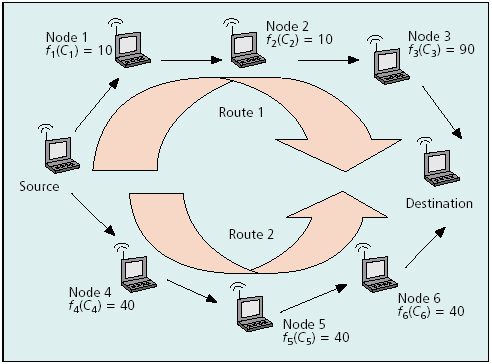
The selection of the best path to minimize the total power needed to route packets and maximize the lifetime of all nodes is the challenge. There are different selection schemes, which are a result of various approaches.
Minimum Total Transmission Power Routing [MTPR]
A successfull transmission requires a signal-to-noise ratio greater than a specific threshold, which is closely related to the bit error rate:
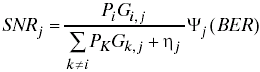
(j – receiver; P – transmission power; G=1/dn – power rolloff between hosts, with n=2 for short and n=4 for longer distance; η – thermal noise; Ψ – threshold).
The influence of noise and distance can be compensated by adjusting of the transmission power. Therefore this power can be used as a metric.
The total transmission power for route l can be derived from:
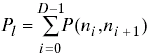
(0 – source; D - destination),
and the route k with minimum total power can be obtained from:
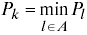
(A – set of all possible routes).
The implementation can be realized by standard shortest path algorithm such as Dijkstra or Bellman-Ford with little modifications for the minimum total power route.
On closer inspection, the algorithm of Dijkstra will select routes with more hops than other routing algorithm, because the transmission power is proportional to dn. This is important to the delay and the route stability.
The solution with the distributed Bellman-Ford algorithm is:
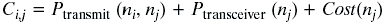
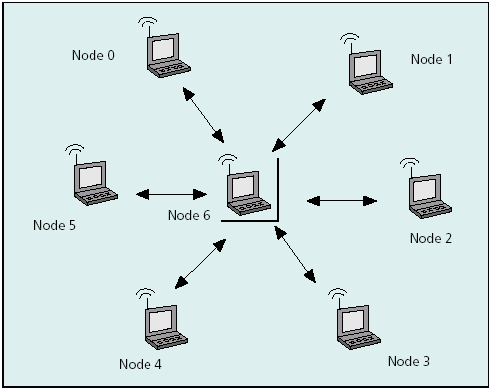
(calculation at j; i – next node on route; Cost – total power cost from source to j),
whereby the power, which will be used when receiving data, is considered.
This value is sent to node i and there the path with the minimum cost is selected:
(NH – set of neighbors).
The procedure is repeated until destination is reached.
This scheme will obtain routes with fewer hops than the modified algorithm of Dijkstra.
The MTPR can reduce the total power consumption of the overall network, but it does not reflect on the lifetime of each host. Because of that, a central host on the route will die soon.
Minimum Battery Cost Routing [MBCR]
With the battery cost function:
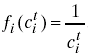
(c – battery capacity at time t ranging between 0 and 100)
the battery cost for route j:
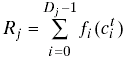
and the route with maximum remaining battery capacity:
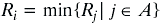
can be calculated.
The MBCR prevents hosts from being overused and increases the time until the network is partitioned. But the selected route can contain nodes with little remaining battery capacity, because only the summation of battery costs is considered.
Min-Max Battery Cost Routing [MMBCR]
The battery cost for route j can be modified/redefined to:
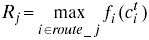
But at the same time the battery cost function and the calculation of the desired route do not change.
The MMBCR tries to avoid nodes with low battery, and by this, the hosts will be used more fairly. Anyway, there is no guarantee that the minimum total transmission power paths will be selected, because the consumption of power can increase by the use of a different way.
Conditional Max-Min Battery Capacity Routing [CMMBCR]
The goals, maximize lifetime of each node and use the battery fairly, cannot achieved simultaneousely by applying MTPR or MMBCR. Generally, this problem is not resolved yet.
A idea is to combine both selection schemes.
By the use of the battery capacity instead of the cost function, the battery capacity for route j at time t can be obtained from:
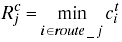
Let A be a set of all routes between any two nodes and satisfying:
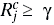
(γ – threshold with range between 0 and 100; can be viewed as protection margin; if battery capacity goes below this, node will be avoided),
and let Q be a set of all possible path between source and destination.
If A∩Q≠∅, which implies that all nodes in some paths have remaining battery capacity higher than γ, then choose a path in A∩Q by applying the MTPR. Otherwise, select the route with the maximum battery capacity:
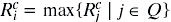
If γ=0, CMMBCR is equal to MTPR, and if γ=100, CMMBCR is equal to MMBCR.
The performance of the CMMBCR will depend on the value of γ.
Performance Considering Power Efficiency
Structure of Simulator
A simulator with the following components and conditions was used to compare the routing algorithms:
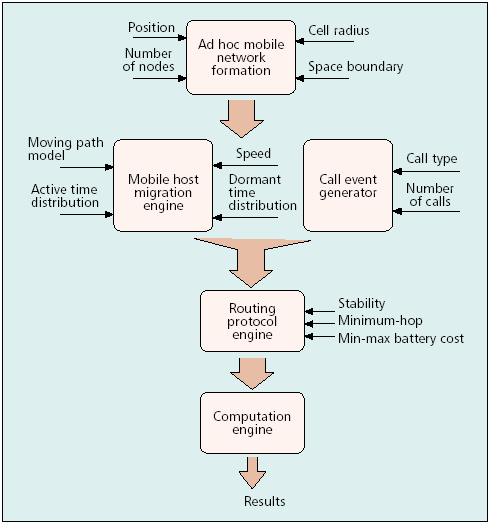
Ad Hoc Mobile Network Formation:
- hosts: 30 (randomly distributed)
- space: 100m x 100m
- cell size: 25m radius
Mobile Host Migration Engine:
- moving direction: randomly (host bounces back at boundary)
- speed: 2m/s
Route Requests Event Generator:
- requests: Poisson process
- source/destination: randomly
- duration: exponentially distributed
Routing Protocols Implementation:
- implementation is simplified (simulation not at packet level)
- selection schemes:
- minimum hop
- stability of route
- MBCR
- MMBCR
- CMMBCR
Power Consumption Computation:
- calculation at the end of each simulation time slot
- power consumption categories:
- communication-related (proportional to traffic)
- non-communication-related (assumed as fix)
- ratio:
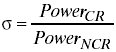
- battery capacity of nodes: the same at the beginning of simulation
- end of simulation: when only two nodes are alive.
Results
time vs. sequence changing σ
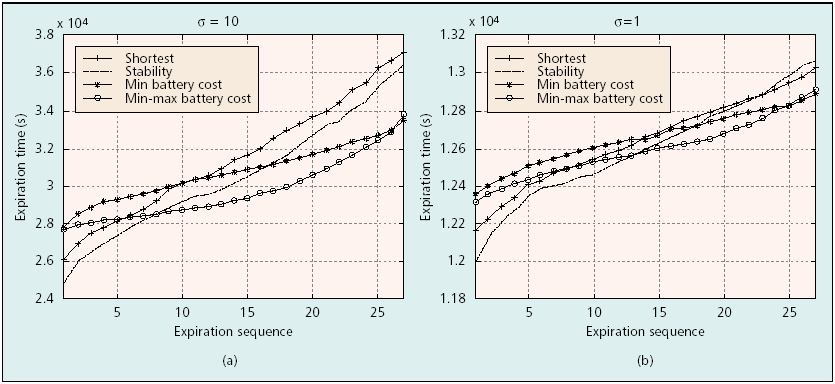
A widely differing power consumption profile for each node is the result of the shortest or the stable path algorithm.
The fair usage of nodes follows by using the MBCR or the MMBCR.
The necessity of power-aware routing decreases as σ decreases.
time vs. sequence changing γ
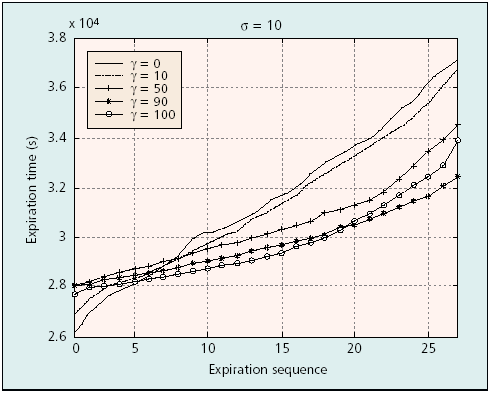
By the value of γ, there is the possibility to choose between the maximization of time when the first node powers down or the maximization of lifetime of the network. The threshold γ can be regarded as an adjusting screw to switch from MTPR to MMBCR.
host lifetime/standard deviation vs. γ
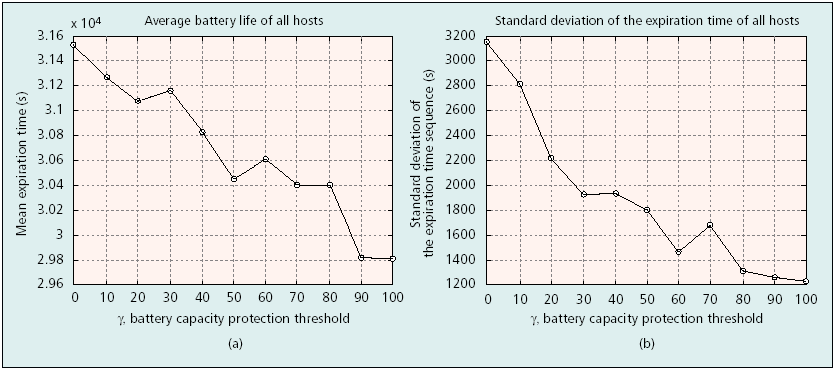
The lifetime of the network and the standard deviation of nodes' lifetime decreases as γ increases. With the protection of nodes at the early stage, there is a high level of fair usage, but the overall power consumption increases by selecting longer paths of alternative routes.
route length vs. γ
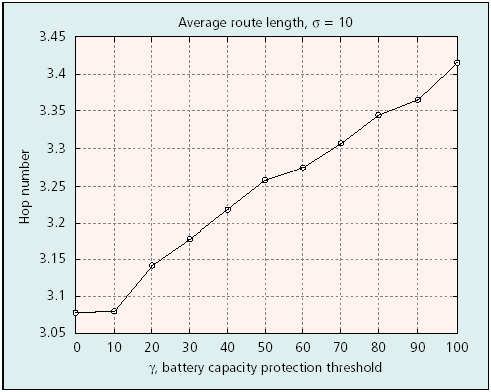
The route length increases as γ increases, because the avoidance of nodes at the early stage result in longer paths of different ways.
Conclusion
Power-aware routing is necessary in ad hoc networks with a lot of communication and limited battery resources of mobile hosts. But there has to be made a trade-off between the fair usage of nodes and the lifetime of the network. A possible solution is the CMMBCR, which combines MTPR and MMBCR by using the threshold γ to switch from one to the other.
Reference
C.-K. Toh, "Maximum Battery Life Routing to Support Ubiquitous Mobile Computing in Wireless Ad Hoc Networks", IEEE Communications Magazin, June 2001