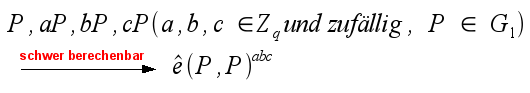Secret Handshakes

[TODO] Einleitung

Mathemathische Grundlagen

Um die nachfolgenden Funktionsweise eines Secret Handshakes besser zu verstehen, gehen wir zunächst kurz auf die verwendeten mathematischen Konstrukte ein.

Gruppen

Eine Gruppe G(M, *) besteht aus einer Menge M und einer Verknüpfung *. Weiterhin ist in der Menge M das neutrale Element der Gruppe G enthalten. Ein Gruppe besitzt ein inverses Element. Abschließend ist die Verknüpfung einer Gruppe assoziativ.

Bei Secret Handshakes werden allerdings zyklische Gruppen verwendet.

zyklische Gruppen

Beispiel (zyklische) Gruppen

Eine endliche zyklische Gruppe G(M, *) heißt zyklisch, wenn die Menge M mindestens ein Element g mit der Eigenschaft M = {g¹, g², g³, ... , g^n} enthält. Man nennt g dann erzeugendes Element der Gruppe. n stellt die Ordnung der Gruppe dar. Gruppen mit einer primen Ordnung q sind immer zyklisch.

bilineare Abbildungen

Ein weiteres wichtiges Thema zum Verständnis der Secret Handshakes sind bilineare Abbildungen.

Eine Abbildung f: E x F → G nennt man bilinear, wenn folgenes gilt:

• für festes x: Die Abbildung f(x, ·): F → G ist linear.
• für festes y: Die Abbildung f(·, y): E → G ist linear.

speziell benötigte lineare Abbildung

das bilineare Diffie-Hellman-Problem

Bei den Secret Handshakes wird eine spezielle bilineare Abbildung ê: G_1 x G_1 → G_2 benötigt. Diese hat muss folgende Eigenschaften besitzen:

• G_1 und G_2 sind zyklische Gruppen mit der Primordnung q
• für alle a, b Element aus Z_q gilt: ê(aP, bQ) = ê(P, Q)^ab

Z_q soll hier für einen Restklassenring stehen.

Modifizierte Weil- und Tate-Paarungen über supersinguläre [elliptische Kurven] sind Beispiele für solche bilineare Abbildungen. Diese sind effizient berechenbar, nicht degenerativ und das bilineare Diffie-Hellman-Problem gilt für sie als schwer berechenbar.

Hashfunktionen

Für die Umsetzung der Secret Handshakes werden nun noch zwei Hashfunktionen benötigt.

erste Hashfuntion: H_1: {0,1}* → G_1

• Abbildung beliebiger Zeichenketten in die zyklische Gruppe G_1

zweite Hashfuntion: H_2: {0,1}* → {0,1}*

• Abbildung beliebiger Zeichenketten in Zeichenketten fester Länge
• kollisionsresistent
• z. B. SHA-1

Allgemeines Prinzip

[TODO]

Pairing Based Handshake Schema

[TODO]

Ablauf im Detail

[TODO]

Sicherheit gegen Abhören

[TODO]

Zusätzliche Eigenschaften

[TODO]

Anpassung des TLS Handshakes

[TODO]

Beweisskizze für die formale Sicherheit

[TODO]

Quellen

• Secret Handshakes from Pairing-Based Key Agreements (2003) Dirk Balfanz, Glenn Durfee, Narendar Shankar, Diana Smetters, Jessica Staddon, Hao-Chi Wong. [1]