Chord

Überblick

Chord ist ein einfaches, verteiltes Suchprotokoll für Peer-To-Peer Systeme, das Schlüssel auf Knoten abbildet. Dabei passt es sich effizient an Strukturveränderungen, wie das Ausfallen oder Hinzukommen von Knoten an und sichert die Funktionalität auch während dieser Anpassung.
Das Protokoll skaliert sowohl in Bezug auf Speicherbedarf, als auch in Bezug auf Kommunikationsaufwand logarithmisch zur Anzahl der Knoten im System.

Chord wird von der Parallel and Distributed Operating Systems Gruppe am MIT Laboratory for Computer Science entwickelt. Hier sind auch Dokumentationen zu den dort durchgeführten Experimenten und Benchmarks, sowie eine Referenzimplementierung erhältlich.

Aufbau von Chord

System Modell

Lastbalanzierung

Chord nutzt Consistent Hashing für eine hinreichend gleichmässige Verteilung der Schlüssel im System.

Dezentralisierung

Alle Knoten im System sind gleichberechtigt.

Skalierbarkeit

Eine Suche benötigt O(log N) Hops, wobei N die Anzahl aller Knoten im System ist.

Verfügbarkeit

Das System passt sich Strukturänderungen an, garantiert dabei aber, dass der für einen Schlüssel zuständige Knoten zu jeder Zeit gefunden wird.

Flexible Namenswahl

Es gibt keine Einschränkungen bezüglich der Struktur bzw. Gestalt der verwendeten Schlüssel.

Topologie

Schlüsselverteilung im Chord Ring

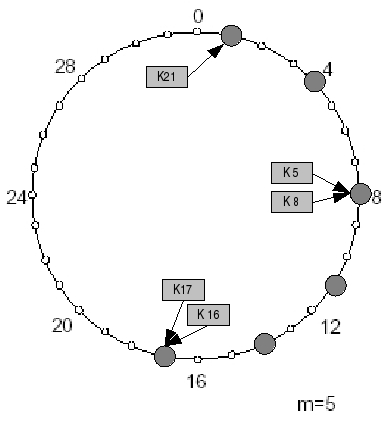
Jedem Knoten und Schlüssel wird eine m-Bit lange ID zugeordnet. Damit können sich maximal 2^m Knoten im System befinden. Diese ID wird mittels einer Basishashfunktion, wie zum Beispiel SHA-1 (hier ist i.A. m=160) berechnet, indem die Hashfunktion auf die IP-Adresse des Knotens bzw. den Schlüssel selbst angewendet wird.
Die Knoten sind in einem Ring modulo 2^m angeordnet. (Chord Ring)
Ein Schlüssel k wird dem Knoten n zugewiesen, dessen ID grösser oder gleich der ID des Schlüssels k ist. Dieser Knoten wird Successor Knoten von k genannt.
Chord bietet nun eine einzige Funktion: Finde den für einen gegebenen Schlüssel k zuständigen Knoten n. Chord bietet keine Funktionalität zur tatsächlichen Speicherung der Daten auf dem zuständigen Knoten.

Einfache Suche

Eine einfache Möglichkeit der Suche nach einem Knoten im Chord Ring, ist die lineare Suche. Jeder Knoten n kennt dabei nur seinen Nachfolgeknoten n' (Successor). Mehr Informationen sind nicht nötig. Wird nun eine Suchanfrage an einen Knoten gerichtet, prüft dieser, ob sein Nachfolgeknoten für den angefragten Schlüssel zuständig ist. Falls ja, ist die Suche beendet. Falls nicht, wird die Anfrage so lange an den jeweils nachfolgenden Knoten weitergereicht, bis das Ziel erreicht ist. n.find_successor(id) if ( id ∈ (n, successor] ) return successor; else return successor.find_successor(id); Pseudo Code für eine einfache Suche Diese Form der Suche ist zwar nicht besonders effizient, da die Länge des Suchpfades linear zur Anzahl der Knoten im System wächst. Aber sie kann jederzeit als Fallback-Variante dienen. Die minimale Vorraussetzung für die lineare Suche, dass jeder Knoten seinen Nachfolgeknoten kennt, ist damit auch die minimale Vorraussetzung für die Korrektheit des Chord Protokolls.

Einfache Suche im Chord Ring

Skalierbare Suche

Finger im Chord Ring

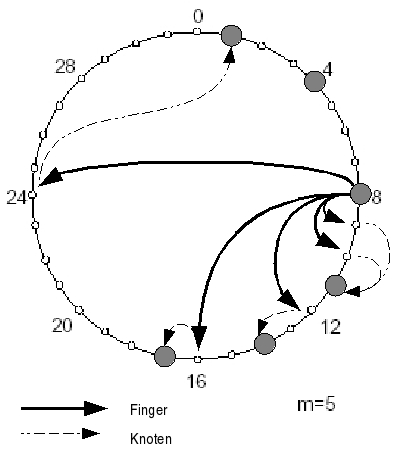
Um die Suche effizienter gestalten zu können, sind weitere Informationen über den Chord-Ring nötig. Deshalb hat jeder Knoten zusätzlich eine Tabelle mit Verweisen auf m weitere Knoten, wobei m die Anzahl der Bits der verwendeten IDs ist. Diese Verweise werden in Chord Finger genannt. Die Tabelle heisst daher Fingertable

Die Fingertable ist wie folgt augebaut:
Der i-te Eintrag der Tabelle auf Knoten n zeigt auf den ersten Knoten, der auf n in einem Abstand von mindestens 2^i-1 folgt.Damit zeigt der letzte Eintrag der Tabelle auf einen Knoten, der mindestens eine halbe Umrundung des Chord-Rings entfernt liegt, der vorletzte auf einen Knoten, der mindestens eine viertel Umrundung entfernt ist, usw. Diese Eigenschaft sichert, dass die maximale Pfadlänge einer Suchanfrage O(log N) Hops beträgt, weil mit jedem Hop die Distanz zum Ziel halbiert werden kann.

# Start Knoten 1 9 11 2 10 11 3 12 14 4 16 17 5 24 1

Aufbau der Fingertable von Knoten n=8 finger[k].Start = (n+2k – 1) mod 2m; (1 ≤ k ≤ m) finger[k].Knoten = erster Knoten ≥ finger[k].Start; successor = finger[1].Knoten;

Pseudo Code für die Suche mit Fingertable

n.find_successor(id) n' = find_predecessor(id); return n'.successor; n.find_predecessor(id) n' = n; while (id ∉ (n', n'.successor]) n' = n'.closest_preceding_finger(id); return n';

/* This is a non-transparent aproach. A transparent version would rather forward the query to the finger-node than access the finger-node directly. */ n.closest_preceding_finger(id) for i = m downto 1 if (finger[i].Knoten ∈ (n, id)) return finger[i].Knoten; return n;

Bei einer Suchanfrage an Knoten n nach Schlüssel k wird nun zunächst der nächstgelegene Vorgänger des Schlüssels gesucht, den Knoten n kennt. Dabei wird die Fingertable so lange von unten nach oben durchsucht, bis der erste Eintrag i gefunden wird, dessen Knoten nicht zwischen n und k liegt. Der Eintrag i+1 ist damit der nächstgelegene Vorgänger von k, den n kennt. Die Suche wird dann mit Hilfe dieses Knotens fortgesetzt. Das wiederholt sich, bis der Knoten gefunden ist, dessen Successor für k zuständig ist.
Wenn zum Beispiel in dem Chord Ring, der auf dem Bild hier zu sehen ist, eine Suchanfrage nach einem Schlüssel mit ID 3 an Knoten 8 gerichtet wird, sucht dieser zunächst den ihm nächstgelegenen, bekannten Vorgängerknoten von 3 (Knoten 1) und richtet die Anfrage an diesen. Knoten 1 stellt fest, dass sein Nachfolgeknoten, Knoten 4, zuständig ist für Schlüssel mit ID 3 und die Suche ist beendet.

Anpassung an Strukturänderungen

Bislang wurde einem bereits bestehenden Chord-Ring ausgegangen, dessen Struktur sich nicht ändert. In realen Anwendungen verhält sich das aber völlig anders. Chord muss mit neu hinzukommenden Knoten genauso fertig werden wie mit Knoten, die spontan ausfallen oder das System ordnungsgemäss verlassen.

Eintritt neuer Knoten

Damit ein neuer Knoten in den Chord-Ring eintreten kann, muss er zunächst einen Einstiegspunkt, also einen Knoten der bereits Teil des Systems ist, finden. Dafür bietet Chord keine Eigene Funktionalität an. In der Regel wird das über well known Knoten oder externe Discovery-Dienste gelöst. Dann wird die die Chord-ID des neuen Knotens berechnet, indem die Hashfunktion beispielsweise auf dessen IP-Adresse angewendet wird. Dann wird eine Suchanfrage am Einstiegsknoten nach dieser ID abgesetzt. Das Resultat dieser Suche ist der Knoten, der direkter Nachfolger (Successor) des neuen Knotens wird. Nachdem der hinzukommende Knoten seinen Successor Zeiger gesetzt hat, muss die Fingertable initialisiert werden. Das kann auf verschiedene Art und Weise von statten gehen. Entweder initialisiert der neue Knoten die Tabelle indem er für jeden Eintrag eine Suche absetzt oder er spart diesen Overhead und kopiert sich die Fingertable seines Successors. Da die Tabelle seines direkten Nachbarn nicht gravierend von der des neuen Knoten abweichen wird, kann getrost diese verwendet werden, bis das Stabilisierungsprotokoll die Tabelle aktualisiert.

Pseudo Code für die Join Operation

n.join(n') predecessor = nil; successor = n'.find_successor(n);

Nachdem die internen Daten initialisiert wurden, muss nun den anderen Knoten im Netzwerk die Existenz dieses neuen Knotens mitgeteilt werden. Das erfolgt als Teil des Stabilisierungsprotokolls, das damit gestartet wird. Chord bietet wie gesagt keine Funktionalität bezüglich des tatsächlichen Speicherns der Daten auf den Knoten. Dementsprechend muss ein Signal an die Anwendung, die das Chord Protokoll nutzt, erfolgen um evtl. Verschieben bzw Kopieren von Daten zu veranlassen, für die vor dem Eintritt des neuen Knotens der Successor zuständig war.