Chord: Difference between revisions
| Line 26: | Line 26: | ||
|Eine einfache Möglichkeit der Suche nach einem Knoten im Chord Ring, ist die lineare Suche. Jeder Knoten <i>n</i> kennt seinen Nachfolgeknoten <i>n'</i> (<i>Successor</i>).<br> |
|Eine einfache Möglichkeit der Suche nach einem Knoten im Chord Ring, ist die lineare Suche. Jeder Knoten <i>n</i> kennt seinen Nachfolgeknoten <i>n'</i> (<i>Successor</i>).<br> |
||
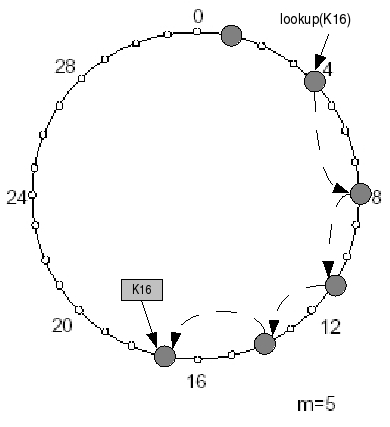
Wird nun eine Suchanfrage an einen Knoten gerichtet, prüft dieser, ob sein Nachfolgeknoten für den angefragten Schlüssel zuständig ist. Falls ja, ist die Suche beendet. Falls nicht, wird die Anfrage so lange an den jeweils nachfolgenden Knoten weitergereicht, bis das Ziel erreicht ist. |
Wird nun eine Suchanfrage an einen Knoten gerichtet, prüft dieser, ob sein Nachfolgeknoten für den angefragten Schlüssel zuständig ist. Falls ja, ist die Suche beendet. Falls nicht, wird die Anfrage so lange an den jeweils nachfolgenden Knoten weitergereicht, bis das Ziel erreicht ist. |
||
{| align="center" |
|||
|- |
|||
| |
|||
n.find_successor(id) |
n.find_successor(id) |
||
if ( id |
if ( id ∈ (n, successor] ) |
||
return successor; |
return successor; |
||
else |
else |
||
return successor.find_successor(id); |
return successor.find_successor(id); |
||
|+ '''Pseudo Code für eine einfache Suche''' |
|||
|} |
|||
Diese Form der Suche ist zwar nicht besonders effizient, da die Länge des Suchpfades linear zur Anzahl der Knoten im System wächst. Aber sie kann jederzeit als Fallback-Variante dienen. Da minimale Vorraussetzung für die lineare Suche, dass jeder Knoten seinen Nachfolgeknoten kennt, ist damit auch die minimale Vorraussetzung für die Korrektheit des Chord Protokolls. |
Diese Form der Suche ist zwar nicht besonders effizient, da die Länge des Suchpfades linear zur Anzahl der Knoten im System wächst. Aber sie kann jederzeit als Fallback-Variante dienen. Da minimale Vorraussetzung für die lineare Suche, dass jeder Knoten seinen Nachfolgeknoten kennt, ist damit auch die minimale Vorraussetzung für die Korrektheit des Chord Protokolls. |
||
||[[Image:ChordLinearSearch.jpg|thumb|250px|Einfache Suche im Chord Ring]] |
||[[Image:ChordLinearSearch.jpg|thumb|250px|Einfache Suche im Chord Ring]] |
||
|} |
|} |
||
== Skalierbare Suche == |
== Skalierbare Suche == |
||
Revision as of 12:34, 1 March 2006
Überblick
Chord ist ein einfaches, verteiltes Suchprotokoll für Peer-To-Peer Systeme, das Schlüssel auf Knoten abbildet. Dabei passt es sich effizient an Strukturveränderungen, wie das Ausfallen oder Hinzukommen von Knoten an und sichert die Funktionalität auch während dieser Anpassung.
Das Protokoll skaliert sowohl in Bezug auf Speicherbedarf, als auch in Bezug auf Kommunikationsaufwand logarithmisch zur Anzahl der Knoten im System.
Chord wird von der Parallel and Distributed Operating Systems Gruppe am MIT Laboratory for Computer Science entwickelt. Hier sind auch Dokumentationen zu den dort durchgeführten Experimenten und Benchmarks, sowie eine Referenzimplementierung erhältlich.
Aufbau von Chord
System Modell
- Lastbalanzierung
- Chord nutzt Consistent Hashing für eine hinreichend gleichmässige Verteilung der Schlüssel im System.
- Dezentralisierung
- Alle Knoten im System sind gleichberechtigt.
- Skalierbarkeit
- Eine Suche benötigt O(log N) Hops, wobei N die Anzahl aller Knoten im System ist.
- Verfügbarkeit
- Das System passt sich Strukturänderungen an, garantiert dabei aber, dass der für einen Schlüssel zuständige Knoten zu jeder Zeit gefunden wird.
- Flexible Namenswahl
- Es gibt keine Einschränkungen bezüglich der Struktur bzw. Gestalt der verwendeten Schlüssel.
Topologie
Jedem Knoten und Schlüssel wird eine m-Bit lange ID zugeordnet. Diese ID wird mittels einer Basishashfunktion, wie zum Beispiel SHA-1 berechnet, indem die Hashfunktion auf die IP-Adresse des Knotens bzw. den Schlüssel selbst angewendet wird.
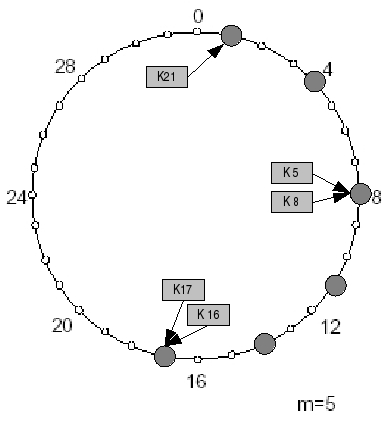
Die Knoten sind in einem Ring modulo 2m angeordnet. (Chord Ring)
Ein Schlüssel k wird dem Knoten n zugewiesen, dessen ID grösser oder gleich der ID des Schlüssels k ist. Dieser Knoten wird Successor Knoten von k genannt.
Chord bietet nun eine einzige Funktion: Finde den für einen gegebenen Schlüssel k zuständigen Knoten n. Chord bietet keine Funktionalität zur tatsächlichen Speicherung der Daten auf dem zuständigen Knoten.