Blind signatures: Difference between revisions
Joanna Rycko (talk | contribs) Texte aus den Folien aus dem ersten Teil hinzugefügt, müssen noch in Lauftext umgeschrieben werden, kommt demnächst |
Joanna Rycko (talk | contribs) mNo edit summary |
||
| Line 1: | Line 1: | ||
'''In Bearbeitung''' |
<span style="color:red;font-size:20pt;text-align:center;margin:20pt">'''In Bearbeitung'''</span> |
||
---- |
|||
== Was ist blinde Unterschrift? == |
== Was ist blinde Unterschrift? == |
||
Revision as of 12:16, 10 July 2007
In Bearbeitung
Was ist blinde Unterschrift?
„Blinde Signatur ist eine Art digitale Unterschrift, bei der der Unterschreibende es nicht sieht, was er unterschreibt.“
Es ist aber nicht so, dass ein Vertrag blind unterschrieben wird. Es geht darum, nicht den Inhalt zu unterschreiben, sondern zu bestätigen, dass ein Dokument von einer bestimmten Person zu einem bestimmten Zeitpunkt vorgelegt wurde (bzw. dass diese Person zu diesem Dokument berechtigt ist).
Zum besseren Verständnis werden im Weiteren zwei Fallstudien vorgestellt, wobei erklärt wird, welche Idee und Zweck hinter den bilnden Signaturen steckt. Es werden auch genaue Arbeitsweise und theoretischen Grundlagen vermittelt.
Wozu blind signature?
Elektronische Wahlen
- I-Voting / Internetwahl / Remote E-Voting
- Deutschland: „Forschungsgruppe Internetwahlen“ » System „i-vote“
- Wahlen zum Studierendenparlament an der Universität Osnabrück, 2001
- Vorstandswahlen des Weimar Kreises, 2005
- USA:
- System „SERVE“ – 2004 Präsidentenwahl; für US-Amerikaner in Übersee und Militäre und ihre Angehörigen
Ein Expertenteam hat dabei festgestellt, dass eine sichere Internetwahl unter gegebenen Bedingungen derzeit unmöglich sei.
Elektronische Zahlungssysteme
- E-Geld: Kartengeld vs. Netzgeld
- DigiCash – Firma von Chaum, 1998 – in Konkurs gegangen und von eCash Technologies übernommen
- Dr David Chaum – über 45 technischen Artikels, über 17 US-Patente
Fallstudie: Wahlsystem
Anforderungen
- Korrektheit der Unterschrift
- Anonymität: blindness und untraceability
- Fälschungssicherheit
- Wahlberechtigungsprüfung
- eine Stimme pro Person zugelassen – Nichtvermehrbarkeit
- Individuelle Verifizierbarkeit
- Universelle Verifizierbarkeit
- geringe Kommunikations- und Rechenkomplexität
Verschiedene Algorithmen
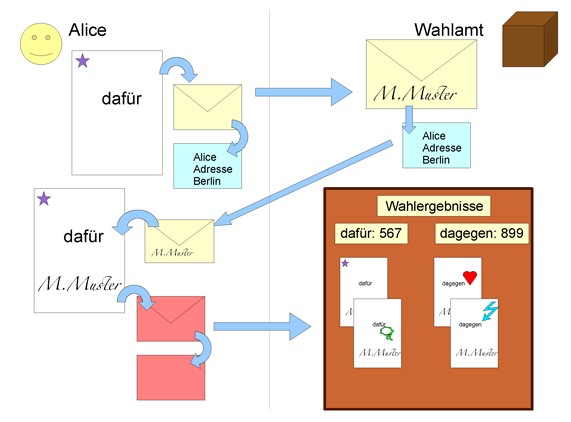
Wahl-Basisidee
Blinde signaturen:
- anonyme Kanale um Stimmzettel zu versenden
- Wahlbehörde überprüft Stimmberechtigung, dann signiert, schickt zurück
- Wähler entfernt persönliche Signatur und schickt an zählende Walbehörde
- Sie prüft Stimmberechtigungssignatur, entschlüsselt und zählt die Stimme
Formaler Ablauf (RSA)
- und – zwei große Primzahlen, vom Signierer (z. B. Wahlamt) geheim gehalten
- – öffentlicher Schlüssel des Signierers
- – privater Schlüssel des Signierers
- – Nachricht (z. B. Stimme), die signiert werden soll
- – blinding factor, z. B. Briefumschlag
- – blinded message
- – unterschriebene blinde Nachricht
- – Signatur
- wird publiziert
- – jeder kann die Legitimität der Unterschrift prüfen
Beispiel p=2, q=5, d=3, e=3, r=3, r-1=7, m=8, alfa=6, t=6, s=2 1=rr-1 mod n 3x7 mod 10 = 1 -> 3x7/10=21/10=2 r. 1 n = 10 ed = 1081 (p-1)(q-1) = 4 rem = 216 alfad = 216 -> t = 6 tr-1 = 6x7 -> s=2
Eigenschaften
Digitale Signatur
- Jeder kann die Authentizität der Signatur nachprüfen
- Signierer kann seine Signatur nicht leugnen
- Sicherheitsbasis – Schwierigkeit der Faktorisierung bzw. Lösung diskreter Logarithmen
- die Unterschrift kann nicht nachgebildet werden
Blinde Signatur
- Signierer weiß nichts über das Verhältnis von „Alice“ und der Nachricht» untraceability
- keine universelle Verifizierbarkeit der Ergebnisse
- ein ausgefüllter kann auf dem Weg zw. Alice und zählender Wahlbehörde verloren gehen falls z.B. der Rechner von Alice ausfällt nachdem die Nachricht bereits signiert wurde
Zahlungssystem
Blinde Signaturen finden eine breite Anwendung in elektronischen Zahlungssystemen wie z.B. einem online Casino. Natürlich stellt sowohl der Betreiber des Casinos als auch der Benutzer gewisse Anforderungen an das System wie Kontrolle und Sicherung der Zahlung oder Fälschungssicherheit des elektronischen Geldes. Eine andere Anwendung von elektronischen Zahlungsmitteln könnte ein Internetshop wie Amazon sein. Dabei könnte man sich vorstellen, dass man sich im Vorfeld von der Bank elektronisches Geld holt (natürlich im Austausch gegen echtes Geld), um damit dann seine Waren zu bezahlen. Ein einfacher Ablauf könnte wie folgt aussehen :
In solch einem System ist es wünschenswert, dass der Zahler seine Anonymität wahrt, d.h. die Bank soll nicht wissen was er wann und bei wem gekauft hat. Dies ist in sofern wichtig, da die Gefahr besteht, dass die Bank ein Kundenprofil vom Kunden anlegt und ggf. die Daten dann gegen ihn verwendet (z.B. bei der Kreditvergabe). Desweiteren muss sichergestellt werden, dass die Echtheit des Geldes leicht verifizierbar ist, denn dies erleichtert die Transaktion für den Verkäufer und fördert Vertrauen. Außerdem soll es unter gewissen Umständen (z.B. Betrug) die Identität des Zahlers zurück zu verfolgen. Es ist zu beachten, dass die letzte Eigenschaft mit der Anonymität nicht in Konflikt steht.
Arten vom digitalen Geld
Digitale Münze
Hierbei handelt es sich um ein Onlineprotokoll, denn eine Münze trägt keine Identifikationsnummer, so dass jedes Mal die Bank die Echtheit der Münze verifizieren muss. Das führt zu einer hohen Netzlast und ist somit für den praktischen Großeinsatz eher nicht geeignet. Ein weiterer Nachteil dieser Münzen ist deren Anonymität, denn dies führt dazu, dass schmutziges Geld (aus Erpressungen, Geldwäsche) nicht mehr zurück zu verfolgen ist. Außerdem besteht ein Problem des Wechselgeldes, so dass ein Münzwert in der Praxis nicht ausreicht.
Digitale Schecks
Bei digitalen Schecks kann der Händler alle Schecks des Kunden sammeln und diese dann gebündelt bei der Bank einreichen, es handelt sich somit um ein Offlineprotokoll. Bei dieser Art vom elektronischen Geld ist ein Betrug des Kunden oder Händlers aufdeckbar. Natürlich muss außerdem sichergestellt werden, dass der Scheck gedeckt ist.
Protokoll von Chaum / Fiat / Naor
Definitionen
• Alice ist der Käufer, Bob der Verkäufer und die Bank ist für die Ausgabe bzw. Aufnahme der digitalen Geldes zuständig.
• Alice stellt zuerst ihre Person als eine Zahl I dar (z.B. ein Hashwert ihrer wichtigsten Daten)
• Sei R die Schecknummer (eine sehr lange Zufallszahl), von Alice erzeugt
• Seien (ai), (bi), (ci) gleichlange Zufallszahlenfolgen , von Alice erzeugt
• Sei h ein Hashfunktion (von der Bank vorgegeben) und xi = h(ai,bi) , yi = h(ai + I, ci) zwei Zahlenfolgen
Ablauf
• Alice erzeugt I, R, (ai), (bi), (ci)
• Die Bank übermittelt die Zahl N und die Hashfunktion h an Alice
• Alice bildet xi = h(ai,bi) , yi = h(ai + I, ci) und übermittelt N Schecks (verblendet) an die Bank, wobei jeder Scheck den Betrag, R, xi und yi enthält
• Die Bank wählt nun N-1 Schecks aus und erfragt die Blindfaktoren, (ai), (bi), (ci) bei Alice, nun kann die Bank auch prüfen, ob Alice wirklich die Wahrheit sagt
• Wenn alle N-1 Schecks in Ordnung sind unterschreibt die Bank den N-ten Scheck blind
• Nun kann Alice mit den unterschriebenen Scheck bei Bob bezahlen
• Bob kann die Unterschrift der Bank mit deren öffentlichen Schlüssel überprüfen
• Bob sendet nun eine N-Bit Zahlenfolge zi an Alice, die für jedes Bit entweder ai, bi und yi (falls zi = 1) oder (ai + 1), ci und xi (falls zi = 0) verrät
• Bob kann nun (xi) und (yi) errechnen und somit den Hashwert des Schecks prüfen
• Bob versendet nun die bestellt Ware, gibt alle Daten der Bank und der entsprechende Betrag wird ihm gutgeschrieben
Eigenschaften des Protokolls
Die Anonymität von Alice gegenüber der Bank ist gewährleistet, denn die Bank kann aus den von Bob erhaltenen Daten nicht aus Alice schließen, d.h. die Bank weiß nicht, dass Alice bei Bobe Waren bestellt hat. Ein Betrug kann aufgedeckt werden, denn wenn Alice mit der selben Münze zwei Mal bezahlt, dann kann die Bank Alice Identität mit großer Wahrscheinlichkeit herausfinden, denn es ist sehr wahrscheinlich, dass die beiden zi sich in einer Stelle unterscheiden. In diesen Fall ist der Bank sowohl ai als auch ai + I bekannt, so dass der Bank I bekannt ist. Dennoch hat das Protokoll einige Restprobleme, denn es besteht ein Sicherheitsrisiko bei weiteren beteiligten (kann durch Verschlüsselung beseitigt werden), die Netzbelastung ist relativ hoch und die Einnahmen von Bob sind nicht anonym, was aber bei Händlern auch nicht der Fall ist. Außerdem besteht das Wechselgeldproblem weiterhin.
Erweiterungen und Fazit
Das Protokoll müsste an die Praxis angepasst werden, denn es müsste mit mehreren Teilnehmern umgehen können. Außerdem ist eine Dezentralisierung und feinere Aufteilung wünschenswert, denn man hat in der realen Welt nicht nur eine zentrale Bank.
Nichtsdestotrotz sind blinde Unterschriften ein relativ neues Forschungsgebiet in der Kryptologie mit einem großen Zukunftspotenzial. Das Unterscheidungsmerkmal von andern z.B. total anonymen Protokollen ist die Sicherstellung und Kontrolle der Transaktionen trotz Anonymität. Diese Eigenschaft ist von besonderer Bedeutung für den Internetverkehr, denn sie deckt Betrügereien auf und macht den Internetzahlungsverkehr sicherer.
Quellen
• Blind signatures for untraceable payments, D. Chaum http://dsns.csie.nctu.edu.tw/research/crypto /HTML/PDF/C82/199.PDF
• Untraceable Electronic Cash, Chaum, Fiat, Naor, 1988 http://www.wisdom.weizmann.ac.il/~naor/PAPERS/untrace_abs.html Abgerufen: 28.05.2007, 23:20
• Untraceable Blind Signature Schemes Based on Discrete Logarithm Problem (2003), Cheng-Chi Lee, Wei-Pang Yang http://portal.acm.org/ft_gateway.cfm?id=1220919&type=pdf& coll=GUIDE&dl=&CFID=15151515&CFTOKEN=6184618
• Elektronisches Geld und elektronische Wahlen, Claudia Ernst, http://www2.informatik.hu-berlin.de/Forschung_Lehre/algorithmenII/ Lehre/WS2005-2006/PS/index.html
• Blind signature. (14.05.2007). In Wikipedia, The Free Encyclopedia. Abgerufen: 16:50, 26.05.2007, http://en.wikipedia.org/w/index.php?title=Blind_signature& oldid=130816222
• DigiCash. (15.05.2007). In Wikipedia, The Free Encyclopedia. Abgerufen 22:22, 28.05.2007, http://en.wikipedia.org/w/index.php?title=DigiCash&oldid=130951311
• I-Voting (6. Mai 2007). In: Wikipedia, Die freie Enzyklopädie. Abgerufen: 28. Mai 2007, 22:26 http://de.wikipedia.org/w/index.php?title=I- Voting&oldid=31456359
• JavaApplet, Wagner 2002, http://www.saar.de/~awa/verdecktus.htm