Chord: Difference between revisions
No edit summary |
|||
| (42 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
= Überblick = |
= Überblick = |
||
Chord ist ein einfaches, verteiltes Suchprotokoll für Peer-To-Peer Systeme, das Schlüssel auf Knoten abbildet. Dabei passt es sich effizient an Strukturveränderungen, wie das Ausfallen oder Hinzukommen von Knoten |
[http://pdos.lcs.mit.edu/chord Chord] ist ein einfaches, verteiltes Suchprotokoll für Peer-To-Peer Systeme, das Schlüssel auf Knoten abbildet. Dabei passt es sich effizient an Strukturveränderungen, wie das Ausfallen oder Hinzukommen von Knoten an und sichert die Funktionalität auch während dieser Anpassung.<br> |
||
Das Protokoll skaliert sowohl in Bezug auf Speicherbedarf, als auch in Bezug auf Kommunikationsaufwand logarithmisch zur Anzahl der Knoten im System. |
Das Protokoll skaliert sowohl in Bezug auf Speicherbedarf, als auch in Bezug auf Kommunikationsaufwand logarithmisch zur Anzahl der Knoten im System. |
||
Chord wird von der [http://pdos.lcs.mit.edu Parallel and Distributed Operating Systems Gruppe] am MIT Laboratory for Computer Science entwickelt. Hier sind auch Dokumentationen zu den dort durchgeführten Experimenten und Benchmarks, sowie eine Referenzimplementierung erhältlich. |
|||
= Aufbau von Chord = |
= Aufbau von Chord = |
||
== System Modell == |
== System Modell == |
||
; Lastbalanzierung: [http://theory.lcs.mit.edu/~karger/Papers/Talks/Hash Consistent Hashing] |
; Lastbalanzierung: Chord nutzt [http://theory.lcs.mit.edu/~karger/Papers/Talks/Hash Consistent Hashing] für eine hinreichend gleichmässige Verteilung der Schlüssel im System. |
||
; Dezentralisierung: Alle Knoten im System sind gleichberechtigt. |
; Dezentralisierung: Alle Knoten im System sind gleichberechtigt. |
||
; Skalierbarkeit: Eine Suche benötigt <i>O(log N)</i> Hops, wobei N die Anzahl aller Knoten im System ist. |
; Skalierbarkeit: Eine Suche benötigt <i>O(log N)</i> Hops, wobei N die Anzahl aller Knoten im System ist. |
||
; Verfügbarkeit: Das System passt sich Strukturänderungen an, garantiert dabei aber, dass der für einen Schlüssel zuständige Knoten zu jeder Zeit gefunden wird. |
; Verfügbarkeit: Das System passt sich Strukturänderungen an, garantiert dabei aber, dass der für einen Schlüssel zuständige Knoten zu jeder Zeit gefunden wird. |
||
; Flexible Namenswahl: Es gibt keine Einschränkungen bezüglich der Struktur bzw. Gestalt der verwendeten Schlüssel. |
; Flexible Namenswahl: Es gibt keine Einschränkungen bezüglich der Struktur bzw. Gestalt der verwendeten Schlüssel. |
||
== Topologie == |
== Topologie == |
||
[[Image:ChordRing.jpg|thumb|left|250px|Schlüsselverteilung im Chord Ring]] |
[[Image:ChordRing.jpg|thumb|left|250px|Schlüsselverteilung im Chord Ring]] |
||
Jedem Knoten und Schlüssel wird eine m-Bit lange ID zugeordnet. Diese ID wird mittels einer Basishashfunktion, wie zum Beispiel [http:// |
Jedem Knoten und Schlüssel wird eine ''m''-Bit lange ID zugeordnet. Damit können sich maximal 2<sup>''m''</sup> Knoten im System befinden. Diese ID wird mittels einer Basishashfunktion, wie zum Beispiel [http://de.wikipedia.org/wiki/SHA1 SHA-1] (hier ist i.A. ''m''=160) berechnet, indem die Hashfunktion auf die IP-Adresse des Knotens bzw. den Schlüssel selbst angewendet wird. <br> |
||
Die Knoten sind in einem Ring modulo 2<sup>m</sup> (<i>Chord Ring</i>) |
Die Knoten sind in einem Ring modulo 2<sup>m</sup> angeordnet. (<i>Chord Ring</i>)<br> |
||
Ein Schlüssel wird dem Knoten zugewiesen, dessen ID |
Ein Schlüssel ''k'' wird dem Knoten ''n'' zugewiesen, dessen ID '''grösser oder gleich''' der ID des Schlüssels ''k'' ist. Dieser Knoten wird <i>Successor Knoten</i> von ''k'' genannt.<br> |
||
Chord bietet nun eine einzige Funktion: Finde den für einen gegebenen Schlüssel <i>k</i> zuständigen Knoten <i>n</i>. Chord bietet keine Funktionalität zur tatsächlichen Speicherung der Daten auf dem zuständigen Knoten. |
|||
<br style="clear:both" /> |
<br style="clear:both" /> |
||
== Einfache Suche == |
== Einfache Suche == |
||
{| |
{| |
||
|Eine einfache Möglichkeit der Suche nach einem Knoten im Chord Ring, ist die lineare Suche. Jeder Knoten <i>n</i> kennt seinen Nachfolgeknoten <i>n'</i> (<i>Successor</i>).<br> |
|Eine einfache Möglichkeit der Suche nach einem Knoten im Chord Ring, ist die lineare Suche. Jeder Knoten <i>n</i> kennt dabei nur seinen Nachfolgeknoten <i>n'</i> (<i>Successor</i>). Mehr Informationen sind nicht nötig.<br> |
||
Wird nun eine Suchanfrage an einen Knoten gerichtet, prüft dieser, ob sein Nachfolgeknoten für den angefragten Schlüssel zuständig ist. Falls ja, ist die Suche beendet. Falls nicht, wird die Anfrage so lange an den jeweils nachfolgenden Knoten weitergereicht, bis das Ziel erreicht ist. |
Wird nun eine Suchanfrage an einen Knoten gerichtet, prüft dieser, ob sein Nachfolgeknoten für den angefragten Schlüssel zuständig ist. Falls ja, ist die Suche beendet. Falls nicht, wird die Anfrage so lange an den jeweils nachfolgenden Knoten weitergereicht, bis das Ziel erreicht ist. |
||
{| align="center" |
|||
|- |
|||
| |
|||
n.find_successor(id) |
n.find_successor(id) |
||
if ( id |
if ( id ∈ (n, successor] ) |
||
return successor; |
return successor; |
||
else |
else |
||
return successor.find_successor(id); |
return successor.find_successor(id); |
||
|+ '''Pseudo Code für eine einfache Suche''' |
|||
Diese Form der Suche ist zwar nicht besonders effizient, da die Länge des Suchpfades linear zur Anzahl der Knoten im System wächst. Aber sie kann jederzeit als Fallback-Variante dienen. Da minimale Vorraussetzung für die lineare Suche, dass jeder Knoten seinen Nachfolgeknoten kennt, ist damit auch die minimale Vorraussetzung für die Korrektheit des Chord Protokolls. |
|||
|} |
|||
Diese Form der Suche ist zwar nicht besonders effizient, da die Länge des Suchpfades linear zur Anzahl der Knoten im System wächst. Aber sie kann jederzeit als Fallback-Variante dienen. Die minimale Voraussetzung für die lineare Suche, dass jeder Knoten seinen Nachfolgeknoten kennt, ist damit auch die minimale Vorraussetzung für die Korrektheit des Chord Protokolls. |
|||
||[[Image:ChordLinearSearch.jpg|thumb|250px|Einfache Suche im Chord Ring]] |
||[[Image:ChordLinearSearch.jpg|thumb|250px|Einfache Suche im Chord Ring]] |
||
|} |
|} |
||
== Skalierbare Suche == |
== Skalierbare Suche == |
||
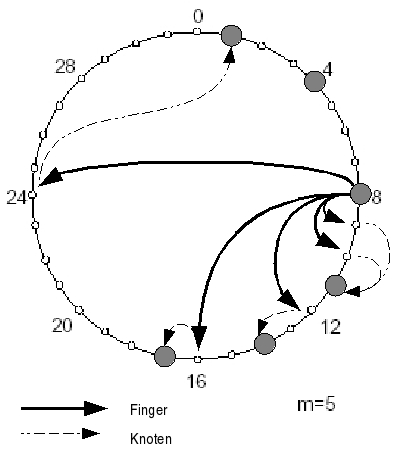
[[Image:ChordFinger.jpg|thumb|right|250px|''Finger'' im Chord Ring ]] |
|||
Um die Suche effizienter gestalten zu können, sind weitere Informationen über den Chord-Ring nötig. Deshalb hat jeder Knoten zusätzlich eine Tabelle mit Verweisen auf ''m'' weitere Knoten, wobei ''m'' die Anzahl der Bits der verwendeten IDs ist. Diese Verweise werden in Chord ''Finger'' genannt. Die Tabelle heisst daher ''Fingertable'' |
|||
Die ''Fingertable'' ist wie folgt augebaut:<br> |
|||
== Eintritt neuer Knoten == |
|||
Der ''Start''-Wert des ''i''-ten Eintrags der Tabelle auf Knoten ''n'' wird mit ''n + 2<sup>i-1</sup>'' belegt. Der ''Knoten''-Wert dieses Eintrags zeigt auf den ersten Knoten, der auf ''n'' in einem Abstand von mindestens 2<sup>i-1</sup> folgt.Damit zeigt der letzte Eintrag der Tabelle auf einen Knoten, der mindestens eine halbe Umrundung des Chord-Rings entfernt liegt, der vorletzte auf einen Knoten, der mindestens eine viertel Umrundung entfernt ist, usw. Diese Eigenschaft sichert, dass die maximale Pfadlänge einer Suchanfrage ''O(log N)'' Hops beträgt, weil mit jedem Hop die Distanz zum Ziel halbiert werden kann. |
|||
{| align="right" cellspacing="10" | |
|||
|- valign="top" | |
|||
| |
|||
{| style="background:#000000;" border="0" cellspacing="1" cellpadding="3" | |
|||
|- align="right" bgcolor="#FFFFFF" | |
|||
! # !! Start !! Knoten |
|||
|- align="right" bgcolor="#DDDDDD" | |
|||
| 1|| 9|| 11 |
|||
|- align="right" bgcolor="#CCCCCC" | |
|||
| 2|| 10|| 11 |
|||
|- align="right" bgcolor="#DDDDDD" | |
|||
| 3|| 12 || 14 |
|||
|- align="right" bgcolor="#CCCCCC" | |
|||
| 4|| 16 || 17 |
|||
|- align="right" bgcolor="#DDDDDD" | |
|||
| 5|| 24 || 1 |
|||
|} |
|||
|| |
|||
{| |
|||
|+ '''Aufbau der Fingertable von Knoten ''n''=8 ''' |
|||
| |
|||
finger[k].Start = (n+2<sup>k – 1</sup>) mod 2<sup>m</sup>; ''(1 ≤ k ≤ m)'' |
|||
finger[k].Knoten = erster Knoten ≥ finger[k].Start; |
|||
successor = finger[1].Knoten; |
|||
|} |
|||
|} |
|||
{| align="right" |
|||
|+ '''Pseudo Code für die Suche mit Fingertable''' |
|||
|- valign="top" |
|||
| |
|||
n.find_successor(id) |
|||
n' = find_predecessor(id); |
|||
return n'.successor; |
|||
n.find_predecessor(id) |
|||
n' = n; |
|||
while (id ∉ (n', n'.successor]) |
|||
n' = n'.closest_preceding_finger(id); |
|||
return n'; |
|||
|| |
|||
/* This is a non-transparent aproach. |
|||
A transparent version would rather |
|||
forward the query to the finger-node |
|||
than access the finger-node directly. */ |
|||
n.closest_preceding_finger(id) |
|||
for i = m downto 1 |
|||
if (finger[i].Knoten ∈ (n, id)) |
|||
return finger[i].Knoten; |
|||
return n; |
|||
|} |
|||
Bei einer Suchanfrage an Knoten ''n'' nach Schlüssel ''k'' wird nun zunächst der nächstgelegene ''Vorgänger'' des Schlüssels gesucht, den Knoten ''n'' kennt. Dabei wird die ''Fingertable'' so lange von '''unten nach oben''' durchsucht, bis der erste Eintrag ''i'' gefunden wird, dessen Knoten '''nicht''' zwischen ''n'' und ''k'' liegt. Der Eintrag ''i+1'' ist damit der nächstgelegene Vorgänger von ''k'', den ''n'' kennt. Die Suche wird dann mit Hilfe dieses Knotens fortgesetzt. Das wiederholt sich, bis der Knoten gefunden ist, dessen ''Successor'' für ''k'' zuständig ist.<br> |
|||
Wenn zum Beispiel in dem Chord Ring, der auf dem Bild hier zu sehen ist, eine Suchanfrage nach einem Schlüssel mit ID 3 an Knoten 8 gerichtet wird, sucht dieser zunächst den ihm nächstgelegenen, bekannten Vorgängerknoten von 3 (Knoten 1) und richtet die Anfrage an diesen. Knoten 1 stellt fest, dass sein Nachfolgeknoten, Knoten 4, zuständig ist für Schlüssel mit ID 3 und die Suche ist beendet. |
|||
<br style="clear:both" /> |
|||
== Anpassung an Strukturänderungen == |
|||
== Stabilisierung == |
|||
Bislang wurde von einem bereits bestehenden Chord-Ring ausgegangen, dessen Struktur sich nicht ändert. In realen Anwendungen verhält sich das aber völlig anders. Chord muss mit neu hinzukommenden Knoten genauso fertig werden wie mit Knoten, die spontan ausfallen oder das System ordnungsgemäss verlassen. Dazu bietet Chord ein robustes Stabilisierungsprotokoll, das auf solche Ereignisse reagiert und die Struktur des Chord-Rings wahrt. Die Anforderungen für ein korrektes Funktionieren des Systems ist minimal: Chord funktioniert so lange korrekt, so lange jeder Knoten seinen Successor erreichen kann. Selbst wenn es nicht der richtige Successor ist, wirkt sich das zwar auf die Länge des Suchpfades aus, da die Suche evtl. einmal um den Ring weitergereicht wird, ein korrektes Auffinden des Knotens ist aber trotzdem sehr wahrscheinlich, da die Stabilisierung in regelmässigen Abständen läuft und diesen Fehler korrigiert. Bei falschen oder fehlenden Finger-Einträgen kann auf die [[#Einfache Suche | einfache Suche]] zurückgegriffen werden. Damit ist die Korrektheit der Fingertable nur für die Perfomance ausschlaggebend. Es kann sogar gezeigt werden: <cite>Wenn zu einem Netzwerk mit N Knoten weitere N Knoten, ohne Fingertable aber mit korrekten Successor Zeigern, hinzukommen, liegt die Anzahl der Hops für eine Suche mit hoher Wahrscheinlichkeit nach wie vor bei O(log N).</cite> Daraus ergibt sich auch die Eigenschaft von Chord, dass selbst während des Stabilisierungsvorgangs Suchanfragen nicht nur korrekt, sondern auch mit sehr geringem Performanceverlust möglich sind. |
|||
== |
=== Stabilisierung === |
||
{| align="right" |
|||
|+ '''Pseudo Code für das Stabilisierungsprotokoll''' |
|||
|- |
|||
| |
|||
n.stabilize() |
|||
x = successor.predecessor; |
|||
if( x ∈ (n, successor) ) |
|||
successor = x; |
|||
successor.notify(n); |
|||
n.notify(n') |
|||
if ( predecessor is nil or n' ∈ (predecessor, n) ) |
|||
predecessor = n'; |
|||
n.fix_fingers() |
|||
for i = 1 to m |
|||
finger[i].Knoten = find_successor(finger[i].Start); |
|||
|} |
|||
Das Stabilisierungsprotokoll von Chord sorgt dafür, dass neue Knoten im restlichen Netzwerk bekannt werden, dass die Fingertable aktualisiert wird und dass die Struktur des Rings erhalten bleibt. Dazu wird zusätzlich zum Successor Pointer und der Fingertable noch ein Zeiger auf den direkten Vorgänger Knoten (''Predecessor'') gespeichert. In Regelmässigen Abständen (z.B. 30 Sekunden) werden dann die Stabilisierungs Routinen ''fix_fingers()'' und ''stabilize()'' gerufen. |
|||
'''fix_fingers()''' setzt für jeden Eintrag der Fingertable eine Suche nach dessen ''Start''-Wert ab und trägt den zuständigen Knoten in die Tabelle ein. Dabei gibt es verschiedene Strategien, wieviele Einträge bei einem Aufruf bearbeitet werden. Es kann bei jedem Aufruf die ganze Tabelle aktualisiert werden, allerdings bedeutet das einiges an Netzwerklast. Es kann aber z.B. auch bei jedem Durchlauf ein zufällig ausgewählter Eintrag erneuert werden. Da die Korrektheit der Fingertable nur für die Performance der Suche, nicht aber für die Korrektheit des Suchergebnisses ausschlaggebend ist, kann man eine nicht ganz aktuelle Fingertable eine gewisse zeit lang tollerieren. |
|||
'''stabilize()''' holt sich den ''Predecessor'' des Nachfolgeknoten. Im Normalfall sollte das der Knoten, an dem die Funktion gerufen wird, selbst sein. Falls allerdings die ID dieses Knotens zwischen der eigenen und des Successors liegt, hat sich offensichtlich die Ringstruktur geändert. In diesem Fall wird der Überprüfte Knoten zum neuen Successor. In jedem Fall aber, wird dem Successor durch den Aufruf der ''notifiy()'' Funktion mitgeteilt, dass der rufende Knoten sich als Predeccessor versteht. Beim Aufruf von '''notifiy()''' überprüft der Knoten an dem die Funktion gerufen wird, ob der bisherige Predecessor entweder nicht verfügbar ist oder die ID des rufenden Knoten zwischen der des bisherigen Predecessors und der eigenen liegt. In diesen beiden Fällen, wird der rufende Knoten als neuer Predecessor eingetragen. |
|||
=== Eintritt neuer Knoten === |
|||
Damit ein neuer Knoten in den Chord-Ring eintreten kann, muss er zunächst einen Einstiegspunkt, also einen Knoten der bereits Teil des Systems ist, finden. Dafür bietet Chord keine Eigene Funktionalität an. In der Regel wird das über ''Well-Known''-Knoten oder externe Discovery-Dienste gelöst. Dann wird die die Chord-ID des neuen Knotens berechnet, indem die Hashfunktion beispielsweise auf dessen IP-Adresse angewendet wird. Dann wird eine Suchanfrage am Einstiegsknoten nach dieser ID abgesetzt. Das Resultat dieser Suche ist der Knoten, der direkter Nachfolger (''Successor'') des neuen Knotens wird. Nachdem der hinzukommende Knoten seinen Successor Zeiger gesetzt hat, muss die Fingertable initialisiert werden. Das kann auf verschiedene Art und Weise von statten gehen. Entweder initialisiert der neue Knoten die Tabelle indem er für jeden Eintrag eine Suche absetzt oder er spart diesen Overhead und kopiert sich die Fingertable seines Successors. Da die Tabelle seines direkten Nachbarn nicht gravierend von der des neuen Knoten abweichen wird, kann getrost diese verwendet werden, bis das [[ #Stabilisierung | Stabilisierungsprotokoll]] die Tabelle aktualisiert. |
|||
{| align="right" |
|||
|+ '''Pseudo Code für die Join Operation''' |
|||
|- |
|||
| |
|||
n.join(n') |
|||
predecessor = nil; |
|||
successor = n'.find_successor(n); |
|||
|} |
|||
Nachdem die internen Daten initialisiert wurden, muss nun den anderen Knoten im Netzwerk die Existenz dieses neuen Knotens mitgeteilt werden. Das erfolgt als Teil des [[ #Stabilisierung | Stabilisierungsprotokolls]] (''notify''), das damit gestartet wird. Chord bietet wie gesagt keine Funktionalität bezüglich des tatsächlichen Speicherns der Daten auf den Knoten. Dementsprechend muss ein Signal an die Anwendung, die das Chord Protokoll nutzt, erfolgen um i.d.R. das Verschieben bzw Kopieren von Daten zu veranlassen, für die vor dem Eintritt des neuen Knotens der Successor zuständig war. Das gilt ebenso evtl Strukturänderungen während der Stabilisierung. |
|||
=== Ausfall & Replikation === |
|||
Wenn ein Knoten den Chord-Ring verlassen möchte, muss er dies seinem Vorgänger- und Nachfolgeknoten mitteilen und evtl. der Anwendungsschicht signalisieren, dass Daten verschoben werden müssen. Bei einem Ausfall eines Knotens passiert das alles jedoch nicht. Damit ist die Prämisse für die Korrektheit von Chord, dass jeder Knoten seinen Nachfolgeknoten erreichen kann, nicht mehr gegeben. Dem wird entgegengewirkt, indem für gewöhnlich neben dem direkten Nachfolgeknoten noch eine List der ''r'' nächsten Nachbarn gespeichert wird. Fällt der Successor-Knoten aus, wird er mit dem ersten erreichbaren Knoten der Liste ersetzt. Damit bei einem Ausfall kein Datenverlust auftritt kann diese Liste auch der Anwendungsschicht bereitestellt werden, um Replikation der Daten zu realisiern. |
|||
= Erweiterungen = |
= Erweiterungen = |
||
==Diminished Chord== |
|||
Diminished Chord ist eine Erweiterung des Chord Protokolls mit der Untergruppen des Chord-Ringes für spezielle Anwendungen geschaffen werden. Der Vorteil dieses Vorgehens besteht in dem geringeren Overhead, da ein globaler Chord-Ring für alle Anwendungen gemeinsam genutzt werden kann und nicht jede Anwendung ihren eigenen bereitstellen muss. Die Performance-Eigenschaften von Chord bleiben dabei auch in den Untergruppen erhalten und der Zusatzaufwand für die Verwaltung der Gruppen ist vernachlässigbar klein. Im wesentlichen stellt Diminished Chord eine einzige Operation bereit: Zu einer Adresse C im Chord-Ring finde den Knoten der Gruppe X mit der nächst höheren Adresse. Dies steht in Analogie zum Protokoll des grundlegenden Chord-Ringes, der ebenfalls im wesentlichen die Operation <i>find_successor</i> bereitstellt. Da es schon mit Chord-Mechanismen in O(log n) möglich ist den allgemeinen Nachfolger einer <i>Adresse</i> zu finden, kann ich mich hier darauf beschränken, den Gruppen-Nachfolger eines <i>Knotens</i> zu suchen. |
|||
===Funktionsweise=== |
|||
====Der Verzeichnisbaum==== |
|||
Ein gemeinsamer, alle Knoten umfassender, im Chord-Ring eingebetteter, Verzeichnisbaum stellt die Gruppen-Suchfunktionen für alle Gruppen bereit. Die Kanten dieses Baumes sind Finger-Zeiger des Chord-Ringes. Der Baum ist binär organisiert und geordnet. Das heißt jeder Elternknoten besitzt eine Chord-Adresse die größer als alle Adressen der Knoten in seinem linken und höchstens so groß wie die kleinste Adresse der Knoten in seinem rechten Unterbaum ist. Jeder Knoten hält zusätzlich Referenzen auf alle Gruppenmitglieder mit den jeweils kleinsten Adressen in seinem rechten Unterbaum. Durch subsequentes Befragen seinter Elternknoten kann nun jeder Knoten seinen nächsten Gruppen-Nachbarn finden. Der maximale Aufwand hierfür ist die Tiefe des Baumes, liegt also in O(log n). Um neue Knoten in eine Gruppe einzufügen, muss nun nur der entsprechende Elternknoten mit dem soeben beschriebenen Verfahren gesucht und benachrichtigt, sowie dessen Gruppeninformationen selktiv übernommen werden. |
|||
====Beispiel==== |
|||
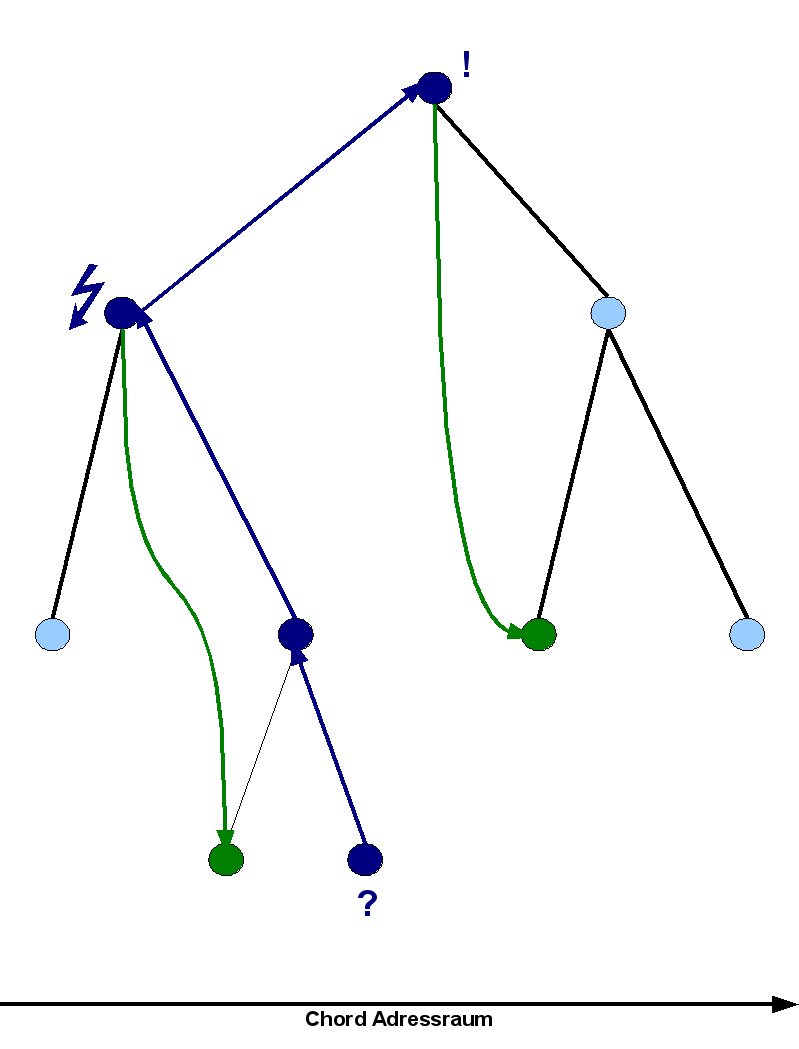
[[Image:DiminishedChordBeispiel.png|right|250px|Suche im Verzeichnisbaum]] |
|||
Um den Suchalgorithmus zu verdeutlichen, kann folgendes Beispiel betrachtet werden. Eine Teilmenge der Knoten im Chord-Ring bildet die Gruppe der "grünen" Knoten. In diesem Fall sind das genau diejenigen Knoten in der Grafik, die grün eingefärbt sind. Elternknoten in deren rechten Teilbäumen grüne Knoten enthalten sind, halten Zeiger auf den jeweils kleinsten davon. Der Knoten "?" sucht nun seinen Nachfolger in der Gruppe der grünen Knoten. Er stellt also eine Anfrage an seinen Eltern-Knoten. Dieser reicht die Anfrage an den Knoten "Blitz" weiter, da er keine grünen Knoten in seimem rechten Unterbaum besitzt. "Blitz" gibt seinen Zeiger auf den grünen Knoten nicht weiter, da dieser sich zwischen der eigenen Adresse und der Adresse der Anfrage befindet. Daher kann es sich nicht um einen Nachfolger handeln. Die Anfrage wird also wiederum weitergereicht und der Knoten "!" findet schließlich den Nachfolger und gibt ihn zurück. |
|||
===Einbettung in den Chord Ring=== |
|||
====Idealisierte Darstellung für "volle" Ringe==== [[Image:DiminishedChordEinbettung.png|left|thumb|350px|Einbettung in den Chord-Ring, aus [http://iptps04.cs.ucsd.edu/papers/karger-subgroup.pdf David R. Karger, Matthias Ruhl, Diminished Chord: A Protocol for Heterogeneous Subgroup Formation in Peer-to-Peer Networks (pdf)], Seite 4]] |
|||
Die Adressen des Chord Ringes werden für diesen Zweck als Gleitkomma-Zahlen im Intervall <math>[0,1]</math> interpretiert. Alle arithmetischen Operationen sind daher "modulo 1" zu verstehen. Außerdem gehe ich idealisierend davon aus, dass alle Adressen im Chord-Ring mit Knoten belegt sind. |
|||
Für jede Untergruppe wird eine Startadresse <math>a_0</math> gewählt. Die Chord-Adresse jedes Knotens wird nun wiederum - für jede Gruppe - als ein Paar <math><a,b></math> ausgedrückt. Für a, b und die Chord-Adresse C des Knotens gilt dabei: <math>C = (a_0 + b/2^a)</math>. Als linkes Kind eines Knotens <math><a,b></math> wird nun der Knoten <math><a+1, 2b-1></math>, als rechtes Kind der Knoten <math><a+1, 2b></math> eingesetzt. Dabei fällt auf, dass die Adresse des rechten Kindes immer gleich der Adresse des Elternknotens ist - jeder Elternknoten ist sein eigenes rechtes Kind - und die Adresse des linken Kindes den Adressraum zwischen dem Elternknoten und dessen Geschwister in zwei gleiche Hälften teilt. Zudem überbrücken Referenzen von (linken) Kinder- auf Eltern-Knoten Zweierpotenzen im Adressraum und sind somit, unter der Annahme, dass alle Adressen mit Knoten belegt sind, Finger im Chord-Ring. Zudem kann ein Kindknoten C allein aus der Startaddresse <math>a_0</math> und seiner eigenen Adresse die Adresse seines Elternknotens berechnen, da es in dem durch die m Bits der Chord-Adresse begrenzten Zahlenraum genau ein Paar <math><a,b></math> gibt, so dass <math>C = a_0 + b/2^a</math> gilt. Aus der so gewonnenen Gruppen-Adresse lässt sich leicht der Elternknoten bestimmen, indem entweder <math><a,b> = <0,0></math> gilt und C schon der Wurzelknoten ist, oder <math><a-1, (b+1)/2></math> den nächsten ("echten") Elternknoten darstellt. |
|||
====Beispiel==== |
|||
[[Image:DiminishedChordEingebettetBeispiel.png|right|250px|Einbettung des Beispiels]] |
|||
Das Beispiel für den Suchalgorithmus kann nun fortgeführt un angepasst werden. Da alle Knoten ihre eigenen rechten Kinder sind verschiebt sich die Baumstruktur wie in der Grafik zu sehen ist. Dabei wird ebenfalls klar, dass der Verzeichnisbaum weiterhin binär und sortiert ist. Weiterhin fällt auf, dass durch das Zusammenfallen der Knoten einerseits die tiefe bis auf das doppelte anwachsen kann, jedoch die Wege der Anfragen im gleichen Maße schrupfen, da die Zeit für das Routing innerhalb eines Knotens als vernachlässigbar gelten kann. Zusätzlich reduziert sich die Zahl der Zeiger auf grüne Knoten, die gespeichert werden muss durch diesen Effekt, da eine Referenz auf einen grünen Knoten nur am „höchsten“ Knoten, der für die Referenz zuständig ist, gespeichert werden muss.<br> |
|||
Da der Chord-Adressraum ringförmig geschlossen ist, wird hier auch deutlich, dass ein spezielles Verfahren nötig ist, um den Nachfolger zu finden, falls die gesuchte Adresse größer ist als die Adresse des größten Gruppenknotens. In diesem Fall wird auch der Wurzelknoten den Nachfolger nicht sofort finden sondern statt dessen seinen linken Unterbaum rekursiv bis zum <i> kleinsten </i> grünen Nachfolger durchsuchen. Da dies jedoch wieder nur O(log n) Schritte - die Tiefe des Baumes - benötigt werden dadurch die Performance-Eigenschaften nicht verzerrt. |
|||
====Verallgemeinerung auf "dünne" Ringe==== |
|||
Um die Idealisierung aufzulösen sind noch einige Zusatzüberlegungen nötig. Aufgaben, die ein nicht existenter Knoten <math><a,b></math> übernehmen müsste, werden von dessen Vorgänger im Chord-Ring <math>p(a,b)</math> übernommen. Das Auffinden der Vorgänger kann ohne zusätzlichen Zeitaufwand in das Chord-Protokoll integriert werden, da der Einfüge-Algorithmus von Chord ohnehin den Vorgänger des einzufügenden Knotens passiert. Durch Verschieben der Zuständigkeit auf Vorgängerknoten, zeigen die Pre-Finger mit Intervallen 2-i unter Umständen nicht mehr genau auf die Elternknoten, sondern auf deren Vorgänger. Dieses Problem lässt sich jedoch durch Testen der Zeiger auf direkte Nachfolger identifizieren und beheben. Obwohl dieses Verfahren bei erster Betrachtung linearen Aufwand zu erzeugen scheint, lässt sich beweisen dass der Gesamtaufwand für die Suche O(log n) nicht übersteigt. Die Strecken die mit linearer Suche überbrückt werden müssen sind vernachlässigbar klein, so lange der Chord-Ring keine unverhältnismäßig großen zusammenhängenden Adressbereiche aufweist, in denen sich keine Knoten befinden. Unter der Annahme, dass die Adressen den Knoten durch eine gute Hash-Funktion zugewiesen werden, ist dies jedoch unwahrscheinlich. |
|||
==Chord#== |
|||
[http://www.zib.de/CSR/Publications/2005-schuett-zr0540.pdf Chord#] ist eine Weiterentwicklung des Chord Protokolls, an der am [http://www.zib.de Zuse Institut Berlin] gearbeitet wird. Die Gleichverteilung der Schlüssel auf Knoten in einem Chord-Ring mittels einer Basis-Hash-Funktion verhindert die Suche nach Intervallen von Schlüsselwerten, da diese auf logisch benachbarten Knoten gespeichert werden müssten. ''Chord#'' eliminiert die Hashfunktion unter Beibehaltung der Perfomance von Chord und ermöglicht damit Bereichsabfragen. |
|||
= Anwendungen = |
= Anwendungen = |
||
==Das Cooperative File System== |
|||
Das Cooperative File System (CFS) ist eine Dateisystem-Schicht die auf dem Chord-Protokoll aufbaut. Dateisystem-Blöcke werden an den Knoten gespeichert, denen das Chord-Protokoll ihre Schlüssel zuordnet. Damit erbt CFS die Performance, Robust heit und Load-Balancing-Eigenschaften in Bezug auf Referenzierung der Daten von Chord. Um die Robustheit auch in Bezug auf die Integrität der Daten zu sichern wird zusätzlich ein Replikationsmechanismus benutzt. Als weitere Performance-Optimierungen sind ebenfalls ein Caching-Schema, ähnlich wie bei Freenet, und "Server Selection" implementiert. Server Selection sorgt dafür, dass Anfragen im Chord-Ring nicht nur andhand der optimalen Finger-Zeiger, sondern auch Anhand von Eigenschaften des physischen Netzes geroutet werden. Führt also der momentan optimale Finger-Zeiger über einen Knoten dessen Netzwerkverbindung eine hohe Latenz aufweist, so kann mittels Server Selection auch der vorige Finger zum Weiterreichen der Anfrage benutzt werden, selbst wenn sich dadurch die Anzahl der Hops erhöht. |
|||
= |
= Siehe Auch = |
||
* [http://pdos.lcs.mit.edu/chord Official Chord Homepage] |
|||
* [http://www.pdos.lcs.mit.edu/papers/chord:sigcomm01/chord_sigcomm.pdf Chord: A Scalable Peer-to-peer Lookup Service for Internet Applications (pdf)] |
|||
* [http://www.zib.de/CSR/Publications/2005-schuett-zr0540.pdf Chord#: Structured Overlay Network for Non-Uniform Load Distribution (pdf)] |
|||
* [http://iptps04.cs.ucsd.edu/papers/karger-subgroup.pdf Diminished Chord: A Protocol for Heterogeneous Subgroup Formation in Peer-to-Peer Networks (pdf)] |
|||
* [http://pdos.csail.mit.edu/papers/cfs:sosp01/cfs_sosp.pdf Wide-area cooperative storage with CFS (pdf)] |
|||
Latest revision as of 19:39, 28 January 2013
Überblick
Chord ist ein einfaches, verteiltes Suchprotokoll für Peer-To-Peer Systeme, das Schlüssel auf Knoten abbildet. Dabei passt es sich effizient an Strukturveränderungen, wie das Ausfallen oder Hinzukommen von Knoten an und sichert die Funktionalität auch während dieser Anpassung.
Das Protokoll skaliert sowohl in Bezug auf Speicherbedarf, als auch in Bezug auf Kommunikationsaufwand logarithmisch zur Anzahl der Knoten im System.
Chord wird von der Parallel and Distributed Operating Systems Gruppe am MIT Laboratory for Computer Science entwickelt. Hier sind auch Dokumentationen zu den dort durchgeführten Experimenten und Benchmarks, sowie eine Referenzimplementierung erhältlich.
Aufbau von Chord
System Modell
- Lastbalanzierung
- Chord nutzt Consistent Hashing für eine hinreichend gleichmässige Verteilung der Schlüssel im System.
- Dezentralisierung
- Alle Knoten im System sind gleichberechtigt.
- Skalierbarkeit
- Eine Suche benötigt O(log N) Hops, wobei N die Anzahl aller Knoten im System ist.
- Verfügbarkeit
- Das System passt sich Strukturänderungen an, garantiert dabei aber, dass der für einen Schlüssel zuständige Knoten zu jeder Zeit gefunden wird.
- Flexible Namenswahl
- Es gibt keine Einschränkungen bezüglich der Struktur bzw. Gestalt der verwendeten Schlüssel.
Topologie
Jedem Knoten und Schlüssel wird eine m-Bit lange ID zugeordnet. Damit können sich maximal 2m Knoten im System befinden. Diese ID wird mittels einer Basishashfunktion, wie zum Beispiel SHA-1 (hier ist i.A. m=160) berechnet, indem die Hashfunktion auf die IP-Adresse des Knotens bzw. den Schlüssel selbst angewendet wird.
Die Knoten sind in einem Ring modulo 2m angeordnet. (Chord Ring)
Ein Schlüssel k wird dem Knoten n zugewiesen, dessen ID grösser oder gleich der ID des Schlüssels k ist. Dieser Knoten wird Successor Knoten von k genannt.
Chord bietet nun eine einzige Funktion: Finde den für einen gegebenen Schlüssel k zuständigen Knoten n. Chord bietet keine Funktionalität zur tatsächlichen Speicherung der Daten auf dem zuständigen Knoten.
Einfache Suche
| Eine einfache Möglichkeit der Suche nach einem Knoten im Chord Ring, ist die lineare Suche. Jeder Knoten n kennt dabei nur seinen Nachfolgeknoten n' (Successor). Mehr Informationen sind nicht nötig. Wird nun eine Suchanfrage an einen Knoten gerichtet, prüft dieser, ob sein Nachfolgeknoten für den angefragten Schlüssel zuständig ist. Falls ja, ist die Suche beendet. Falls nicht, wird die Anfrage so lange an den jeweils nachfolgenden Knoten weitergereicht, bis das Ziel erreicht ist.
Diese Form der Suche ist zwar nicht besonders effizient, da die Länge des Suchpfades linear zur Anzahl der Knoten im System wächst. Aber sie kann jederzeit als Fallback-Variante dienen. Die minimale Voraussetzung für die lineare Suche, dass jeder Knoten seinen Nachfolgeknoten kennt, ist damit auch die minimale Vorraussetzung für die Korrektheit des Chord Protokolls. |
Skalierbare Suche
Um die Suche effizienter gestalten zu können, sind weitere Informationen über den Chord-Ring nötig. Deshalb hat jeder Knoten zusätzlich eine Tabelle mit Verweisen auf m weitere Knoten, wobei m die Anzahl der Bits der verwendeten IDs ist. Diese Verweise werden in Chord Finger genannt. Die Tabelle heisst daher Fingertable
Die Fingertable ist wie folgt augebaut:
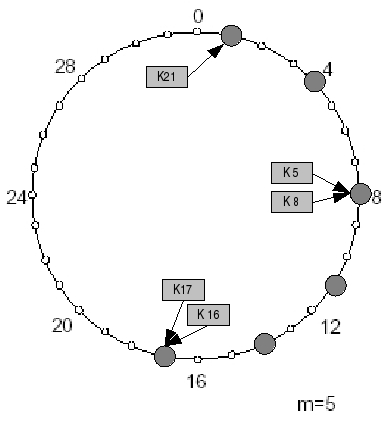
Der Start-Wert des i-ten Eintrags der Tabelle auf Knoten n wird mit n + 2i-1 belegt. Der Knoten-Wert dieses Eintrags zeigt auf den ersten Knoten, der auf n in einem Abstand von mindestens 2i-1 folgt.Damit zeigt der letzte Eintrag der Tabelle auf einen Knoten, der mindestens eine halbe Umrundung des Chord-Rings entfernt liegt, der vorletzte auf einen Knoten, der mindestens eine viertel Umrundung entfernt ist, usw. Diese Eigenschaft sichert, dass die maximale Pfadlänge einer Suchanfrage O(log N) Hops beträgt, weil mit jedem Hop die Distanz zum Ziel halbiert werden kann.
|
|
n.find_successor(id)
n' = find_predecessor(id);
return n'.successor;
n.find_predecessor(id)
n' = n;
while (id ∉ (n', n'.successor])
n' = n'.closest_preceding_finger(id);
return n';
|
/* This is a non-transparent aproach.
A transparent version would rather
forward the query to the finger-node
than access the finger-node directly. */
n.closest_preceding_finger(id)
for i = m downto 1
if (finger[i].Knoten ∈ (n, id))
return finger[i].Knoten;
return n;
|
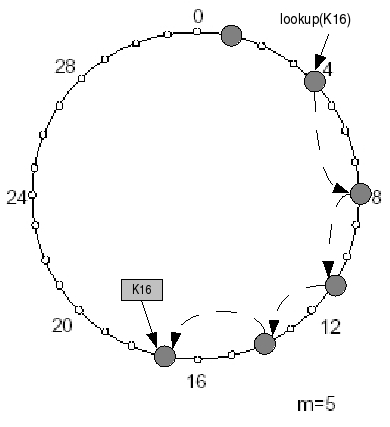
Bei einer Suchanfrage an Knoten n nach Schlüssel k wird nun zunächst der nächstgelegene Vorgänger des Schlüssels gesucht, den Knoten n kennt. Dabei wird die Fingertable so lange von unten nach oben durchsucht, bis der erste Eintrag i gefunden wird, dessen Knoten nicht zwischen n und k liegt. Der Eintrag i+1 ist damit der nächstgelegene Vorgänger von k, den n kennt. Die Suche wird dann mit Hilfe dieses Knotens fortgesetzt. Das wiederholt sich, bis der Knoten gefunden ist, dessen Successor für k zuständig ist.
Wenn zum Beispiel in dem Chord Ring, der auf dem Bild hier zu sehen ist, eine Suchanfrage nach einem Schlüssel mit ID 3 an Knoten 8 gerichtet wird, sucht dieser zunächst den ihm nächstgelegenen, bekannten Vorgängerknoten von 3 (Knoten 1) und richtet die Anfrage an diesen. Knoten 1 stellt fest, dass sein Nachfolgeknoten, Knoten 4, zuständig ist für Schlüssel mit ID 3 und die Suche ist beendet.
Anpassung an Strukturänderungen
Bislang wurde von einem bereits bestehenden Chord-Ring ausgegangen, dessen Struktur sich nicht ändert. In realen Anwendungen verhält sich das aber völlig anders. Chord muss mit neu hinzukommenden Knoten genauso fertig werden wie mit Knoten, die spontan ausfallen oder das System ordnungsgemäss verlassen. Dazu bietet Chord ein robustes Stabilisierungsprotokoll, das auf solche Ereignisse reagiert und die Struktur des Chord-Rings wahrt. Die Anforderungen für ein korrektes Funktionieren des Systems ist minimal: Chord funktioniert so lange korrekt, so lange jeder Knoten seinen Successor erreichen kann. Selbst wenn es nicht der richtige Successor ist, wirkt sich das zwar auf die Länge des Suchpfades aus, da die Suche evtl. einmal um den Ring weitergereicht wird, ein korrektes Auffinden des Knotens ist aber trotzdem sehr wahrscheinlich, da die Stabilisierung in regelmässigen Abständen läuft und diesen Fehler korrigiert. Bei falschen oder fehlenden Finger-Einträgen kann auf die einfache Suche zurückgegriffen werden. Damit ist die Korrektheit der Fingertable nur für die Perfomance ausschlaggebend. Es kann sogar gezeigt werden: Wenn zu einem Netzwerk mit N Knoten weitere N Knoten, ohne Fingertable aber mit korrekten Successor Zeigern, hinzukommen, liegt die Anzahl der Hops für eine Suche mit hoher Wahrscheinlichkeit nach wie vor bei O(log N). Daraus ergibt sich auch die Eigenschaft von Chord, dass selbst während des Stabilisierungsvorgangs Suchanfragen nicht nur korrekt, sondern auch mit sehr geringem Performanceverlust möglich sind.
Stabilisierung
n.stabilize()
x = successor.predecessor;
if( x ∈ (n, successor) )
successor = x;
successor.notify(n);
n.notify(n')
if ( predecessor is nil or n' ∈ (predecessor, n) )
predecessor = n';
n.fix_fingers()
for i = 1 to m
finger[i].Knoten = find_successor(finger[i].Start);
|
Das Stabilisierungsprotokoll von Chord sorgt dafür, dass neue Knoten im restlichen Netzwerk bekannt werden, dass die Fingertable aktualisiert wird und dass die Struktur des Rings erhalten bleibt. Dazu wird zusätzlich zum Successor Pointer und der Fingertable noch ein Zeiger auf den direkten Vorgänger Knoten (Predecessor) gespeichert. In Regelmässigen Abständen (z.B. 30 Sekunden) werden dann die Stabilisierungs Routinen fix_fingers() und stabilize() gerufen.
fix_fingers() setzt für jeden Eintrag der Fingertable eine Suche nach dessen Start-Wert ab und trägt den zuständigen Knoten in die Tabelle ein. Dabei gibt es verschiedene Strategien, wieviele Einträge bei einem Aufruf bearbeitet werden. Es kann bei jedem Aufruf die ganze Tabelle aktualisiert werden, allerdings bedeutet das einiges an Netzwerklast. Es kann aber z.B. auch bei jedem Durchlauf ein zufällig ausgewählter Eintrag erneuert werden. Da die Korrektheit der Fingertable nur für die Performance der Suche, nicht aber für die Korrektheit des Suchergebnisses ausschlaggebend ist, kann man eine nicht ganz aktuelle Fingertable eine gewisse zeit lang tollerieren.
stabilize() holt sich den Predecessor des Nachfolgeknoten. Im Normalfall sollte das der Knoten, an dem die Funktion gerufen wird, selbst sein. Falls allerdings die ID dieses Knotens zwischen der eigenen und des Successors liegt, hat sich offensichtlich die Ringstruktur geändert. In diesem Fall wird der Überprüfte Knoten zum neuen Successor. In jedem Fall aber, wird dem Successor durch den Aufruf der notifiy() Funktion mitgeteilt, dass der rufende Knoten sich als Predeccessor versteht. Beim Aufruf von notifiy() überprüft der Knoten an dem die Funktion gerufen wird, ob der bisherige Predecessor entweder nicht verfügbar ist oder die ID des rufenden Knoten zwischen der des bisherigen Predecessors und der eigenen liegt. In diesen beiden Fällen, wird der rufende Knoten als neuer Predecessor eingetragen.
Eintritt neuer Knoten
Damit ein neuer Knoten in den Chord-Ring eintreten kann, muss er zunächst einen Einstiegspunkt, also einen Knoten der bereits Teil des Systems ist, finden. Dafür bietet Chord keine Eigene Funktionalität an. In der Regel wird das über Well-Known-Knoten oder externe Discovery-Dienste gelöst. Dann wird die die Chord-ID des neuen Knotens berechnet, indem die Hashfunktion beispielsweise auf dessen IP-Adresse angewendet wird. Dann wird eine Suchanfrage am Einstiegsknoten nach dieser ID abgesetzt. Das Resultat dieser Suche ist der Knoten, der direkter Nachfolger (Successor) des neuen Knotens wird. Nachdem der hinzukommende Knoten seinen Successor Zeiger gesetzt hat, muss die Fingertable initialisiert werden. Das kann auf verschiedene Art und Weise von statten gehen. Entweder initialisiert der neue Knoten die Tabelle indem er für jeden Eintrag eine Suche absetzt oder er spart diesen Overhead und kopiert sich die Fingertable seines Successors. Da die Tabelle seines direkten Nachbarn nicht gravierend von der des neuen Knoten abweichen wird, kann getrost diese verwendet werden, bis das Stabilisierungsprotokoll die Tabelle aktualisiert.
n.join(n') predecessor = nil; successor = n'.find_successor(n); |
Nachdem die internen Daten initialisiert wurden, muss nun den anderen Knoten im Netzwerk die Existenz dieses neuen Knotens mitgeteilt werden. Das erfolgt als Teil des Stabilisierungsprotokolls (notify), das damit gestartet wird. Chord bietet wie gesagt keine Funktionalität bezüglich des tatsächlichen Speicherns der Daten auf den Knoten. Dementsprechend muss ein Signal an die Anwendung, die das Chord Protokoll nutzt, erfolgen um i.d.R. das Verschieben bzw Kopieren von Daten zu veranlassen, für die vor dem Eintritt des neuen Knotens der Successor zuständig war. Das gilt ebenso evtl Strukturänderungen während der Stabilisierung.
Ausfall & Replikation
Wenn ein Knoten den Chord-Ring verlassen möchte, muss er dies seinem Vorgänger- und Nachfolgeknoten mitteilen und evtl. der Anwendungsschicht signalisieren, dass Daten verschoben werden müssen. Bei einem Ausfall eines Knotens passiert das alles jedoch nicht. Damit ist die Prämisse für die Korrektheit von Chord, dass jeder Knoten seinen Nachfolgeknoten erreichen kann, nicht mehr gegeben. Dem wird entgegengewirkt, indem für gewöhnlich neben dem direkten Nachfolgeknoten noch eine List der r nächsten Nachbarn gespeichert wird. Fällt der Successor-Knoten aus, wird er mit dem ersten erreichbaren Knoten der Liste ersetzt. Damit bei einem Ausfall kein Datenverlust auftritt kann diese Liste auch der Anwendungsschicht bereitestellt werden, um Replikation der Daten zu realisiern.
Erweiterungen
Diminished Chord
Diminished Chord ist eine Erweiterung des Chord Protokolls mit der Untergruppen des Chord-Ringes für spezielle Anwendungen geschaffen werden. Der Vorteil dieses Vorgehens besteht in dem geringeren Overhead, da ein globaler Chord-Ring für alle Anwendungen gemeinsam genutzt werden kann und nicht jede Anwendung ihren eigenen bereitstellen muss. Die Performance-Eigenschaften von Chord bleiben dabei auch in den Untergruppen erhalten und der Zusatzaufwand für die Verwaltung der Gruppen ist vernachlässigbar klein. Im wesentlichen stellt Diminished Chord eine einzige Operation bereit: Zu einer Adresse C im Chord-Ring finde den Knoten der Gruppe X mit der nächst höheren Adresse. Dies steht in Analogie zum Protokoll des grundlegenden Chord-Ringes, der ebenfalls im wesentlichen die Operation find_successor bereitstellt. Da es schon mit Chord-Mechanismen in O(log n) möglich ist den allgemeinen Nachfolger einer Adresse zu finden, kann ich mich hier darauf beschränken, den Gruppen-Nachfolger eines Knotens zu suchen.
Funktionsweise
Der Verzeichnisbaum
Ein gemeinsamer, alle Knoten umfassender, im Chord-Ring eingebetteter, Verzeichnisbaum stellt die Gruppen-Suchfunktionen für alle Gruppen bereit. Die Kanten dieses Baumes sind Finger-Zeiger des Chord-Ringes. Der Baum ist binär organisiert und geordnet. Das heißt jeder Elternknoten besitzt eine Chord-Adresse die größer als alle Adressen der Knoten in seinem linken und höchstens so groß wie die kleinste Adresse der Knoten in seinem rechten Unterbaum ist. Jeder Knoten hält zusätzlich Referenzen auf alle Gruppenmitglieder mit den jeweils kleinsten Adressen in seinem rechten Unterbaum. Durch subsequentes Befragen seinter Elternknoten kann nun jeder Knoten seinen nächsten Gruppen-Nachbarn finden. Der maximale Aufwand hierfür ist die Tiefe des Baumes, liegt also in O(log n). Um neue Knoten in eine Gruppe einzufügen, muss nun nur der entsprechende Elternknoten mit dem soeben beschriebenen Verfahren gesucht und benachrichtigt, sowie dessen Gruppeninformationen selktiv übernommen werden.
Beispiel
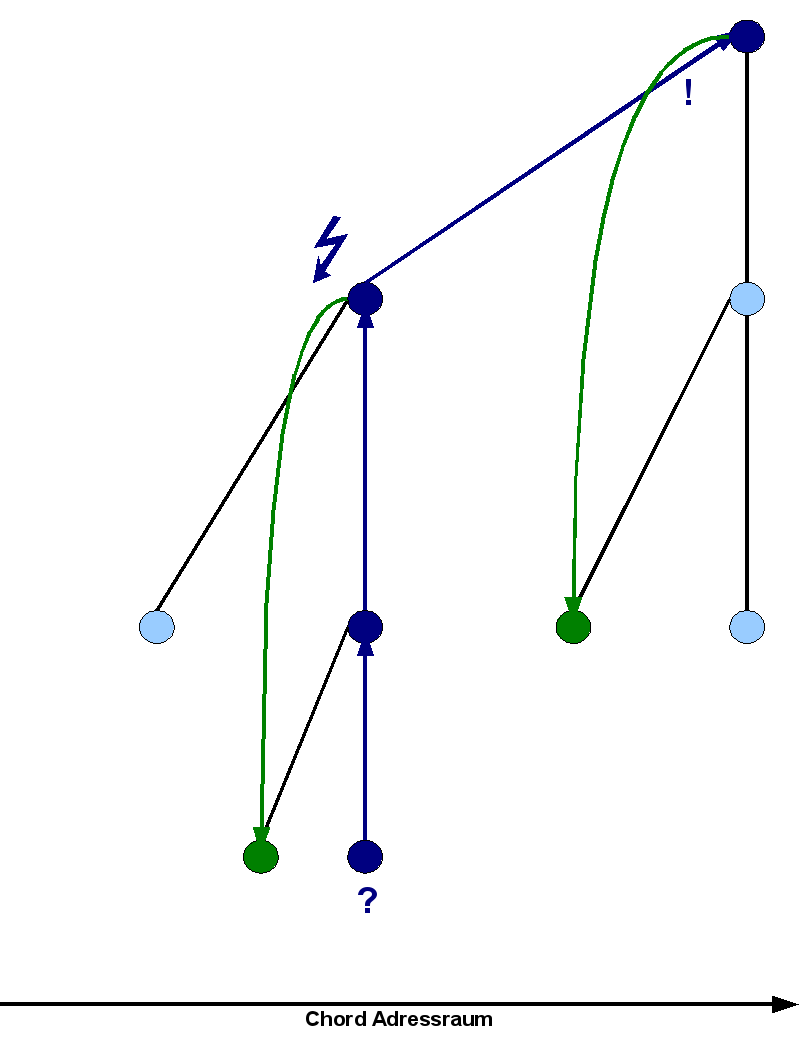
Um den Suchalgorithmus zu verdeutlichen, kann folgendes Beispiel betrachtet werden. Eine Teilmenge der Knoten im Chord-Ring bildet die Gruppe der "grünen" Knoten. In diesem Fall sind das genau diejenigen Knoten in der Grafik, die grün eingefärbt sind. Elternknoten in deren rechten Teilbäumen grüne Knoten enthalten sind, halten Zeiger auf den jeweils kleinsten davon. Der Knoten "?" sucht nun seinen Nachfolger in der Gruppe der grünen Knoten. Er stellt also eine Anfrage an seinen Eltern-Knoten. Dieser reicht die Anfrage an den Knoten "Blitz" weiter, da er keine grünen Knoten in seimem rechten Unterbaum besitzt. "Blitz" gibt seinen Zeiger auf den grünen Knoten nicht weiter, da dieser sich zwischen der eigenen Adresse und der Adresse der Anfrage befindet. Daher kann es sich nicht um einen Nachfolger handeln. Die Anfrage wird also wiederum weitergereicht und der Knoten "!" findet schließlich den Nachfolger und gibt ihn zurück.
Einbettung in den Chord Ring
====Idealisierte Darstellung für "volle" Ringe====
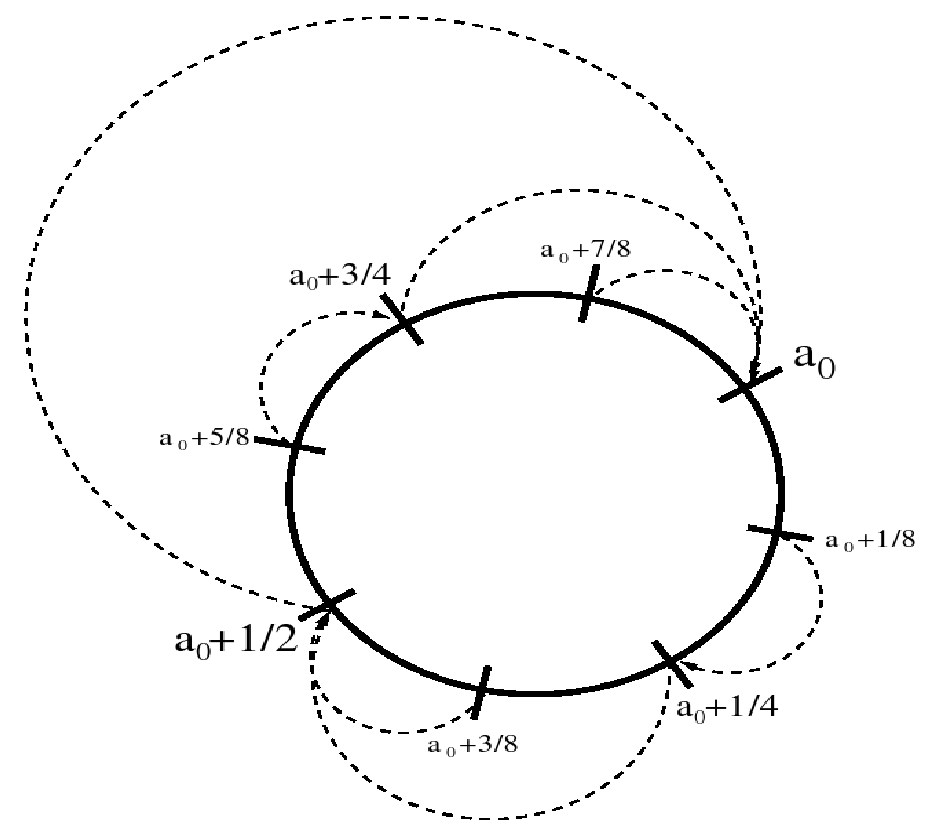
Die Adressen des Chord Ringes werden für diesen Zweck als Gleitkomma-Zahlen im Intervall interpretiert. Alle arithmetischen Operationen sind daher "modulo 1" zu verstehen. Außerdem gehe ich idealisierend davon aus, dass alle Adressen im Chord-Ring mit Knoten belegt sind. Für jede Untergruppe wird eine Startadresse gewählt. Die Chord-Adresse jedes Knotens wird nun wiederum - für jede Gruppe - als ein Paar ausgedrückt. Für a, b und die Chord-Adresse C des Knotens gilt dabei: . Als linkes Kind eines Knotens wird nun der Knoten , als rechtes Kind der Knoten eingesetzt. Dabei fällt auf, dass die Adresse des rechten Kindes immer gleich der Adresse des Elternknotens ist - jeder Elternknoten ist sein eigenes rechtes Kind - und die Adresse des linken Kindes den Adressraum zwischen dem Elternknoten und dessen Geschwister in zwei gleiche Hälften teilt. Zudem überbrücken Referenzen von (linken) Kinder- auf Eltern-Knoten Zweierpotenzen im Adressraum und sind somit, unter der Annahme, dass alle Adressen mit Knoten belegt sind, Finger im Chord-Ring. Zudem kann ein Kindknoten C allein aus der Startaddresse und seiner eigenen Adresse die Adresse seines Elternknotens berechnen, da es in dem durch die m Bits der Chord-Adresse begrenzten Zahlenraum genau ein Paar gibt, so dass gilt. Aus der so gewonnenen Gruppen-Adresse lässt sich leicht der Elternknoten bestimmen, indem entweder gilt und C schon der Wurzelknoten ist, oder den nächsten ("echten") Elternknoten darstellt.
Beispiel
Das Beispiel für den Suchalgorithmus kann nun fortgeführt un angepasst werden. Da alle Knoten ihre eigenen rechten Kinder sind verschiebt sich die Baumstruktur wie in der Grafik zu sehen ist. Dabei wird ebenfalls klar, dass der Verzeichnisbaum weiterhin binär und sortiert ist. Weiterhin fällt auf, dass durch das Zusammenfallen der Knoten einerseits die tiefe bis auf das doppelte anwachsen kann, jedoch die Wege der Anfragen im gleichen Maße schrupfen, da die Zeit für das Routing innerhalb eines Knotens als vernachlässigbar gelten kann. Zusätzlich reduziert sich die Zahl der Zeiger auf grüne Knoten, die gespeichert werden muss durch diesen Effekt, da eine Referenz auf einen grünen Knoten nur am „höchsten“ Knoten, der für die Referenz zuständig ist, gespeichert werden muss.
Da der Chord-Adressraum ringförmig geschlossen ist, wird hier auch deutlich, dass ein spezielles Verfahren nötig ist, um den Nachfolger zu finden, falls die gesuchte Adresse größer ist als die Adresse des größten Gruppenknotens. In diesem Fall wird auch der Wurzelknoten den Nachfolger nicht sofort finden sondern statt dessen seinen linken Unterbaum rekursiv bis zum kleinsten grünen Nachfolger durchsuchen. Da dies jedoch wieder nur O(log n) Schritte - die Tiefe des Baumes - benötigt werden dadurch die Performance-Eigenschaften nicht verzerrt.
Verallgemeinerung auf "dünne" Ringe
Um die Idealisierung aufzulösen sind noch einige Zusatzüberlegungen nötig. Aufgaben, die ein nicht existenter Knoten übernehmen müsste, werden von dessen Vorgänger im Chord-Ring übernommen. Das Auffinden der Vorgänger kann ohne zusätzlichen Zeitaufwand in das Chord-Protokoll integriert werden, da der Einfüge-Algorithmus von Chord ohnehin den Vorgänger des einzufügenden Knotens passiert. Durch Verschieben der Zuständigkeit auf Vorgängerknoten, zeigen die Pre-Finger mit Intervallen 2-i unter Umständen nicht mehr genau auf die Elternknoten, sondern auf deren Vorgänger. Dieses Problem lässt sich jedoch durch Testen der Zeiger auf direkte Nachfolger identifizieren und beheben. Obwohl dieses Verfahren bei erster Betrachtung linearen Aufwand zu erzeugen scheint, lässt sich beweisen dass der Gesamtaufwand für die Suche O(log n) nicht übersteigt. Die Strecken die mit linearer Suche überbrückt werden müssen sind vernachlässigbar klein, so lange der Chord-Ring keine unverhältnismäßig großen zusammenhängenden Adressbereiche aufweist, in denen sich keine Knoten befinden. Unter der Annahme, dass die Adressen den Knoten durch eine gute Hash-Funktion zugewiesen werden, ist dies jedoch unwahrscheinlich.
Chord#
Chord# ist eine Weiterentwicklung des Chord Protokolls, an der am Zuse Institut Berlin gearbeitet wird. Die Gleichverteilung der Schlüssel auf Knoten in einem Chord-Ring mittels einer Basis-Hash-Funktion verhindert die Suche nach Intervallen von Schlüsselwerten, da diese auf logisch benachbarten Knoten gespeichert werden müssten. Chord# eliminiert die Hashfunktion unter Beibehaltung der Perfomance von Chord und ermöglicht damit Bereichsabfragen.
Anwendungen
Das Cooperative File System
Das Cooperative File System (CFS) ist eine Dateisystem-Schicht die auf dem Chord-Protokoll aufbaut. Dateisystem-Blöcke werden an den Knoten gespeichert, denen das Chord-Protokoll ihre Schlüssel zuordnet. Damit erbt CFS die Performance, Robust heit und Load-Balancing-Eigenschaften in Bezug auf Referenzierung der Daten von Chord. Um die Robustheit auch in Bezug auf die Integrität der Daten zu sichern wird zusätzlich ein Replikationsmechanismus benutzt. Als weitere Performance-Optimierungen sind ebenfalls ein Caching-Schema, ähnlich wie bei Freenet, und "Server Selection" implementiert. Server Selection sorgt dafür, dass Anfragen im Chord-Ring nicht nur andhand der optimalen Finger-Zeiger, sondern auch Anhand von Eigenschaften des physischen Netzes geroutet werden. Führt also der momentan optimale Finger-Zeiger über einen Knoten dessen Netzwerkverbindung eine hohe Latenz aufweist, so kann mittels Server Selection auch der vorige Finger zum Weiterreichen der Anfrage benutzt werden, selbst wenn sich dadurch die Anzahl der Hops erhöht.
Siehe Auch
- Official Chord Homepage
- Chord: A Scalable Peer-to-peer Lookup Service for Internet Applications (pdf)
- Chord#: Structured Overlay Network for Non-Uniform Load Distribution (pdf)
- Diminished Chord: A Protocol for Heterogeneous Subgroup Formation in Peer-to-Peer Networks (pdf)
- Wide-area cooperative storage with CFS (pdf)
![{\displaystyle [0,1]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)