DART - Dynamic Address Routing: Difference between revisions
No edit summary |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
== Address space == |
== Address space == |
||
[[Image:AddressTree.JPG|thumb| |
[[Image:AddressTree.JPG|thumb|right|250px|The Address Tree of a 3-bit binary address]] The ''Address Tree'' is an abstract visualization from the address space point of view. Its leaves represent peers in a network by their addresses. Its inner nodes represent address subtrees. An address subtree consists of nodes with the same address prefix. The dotted lines in the example image indicate physical links (wired or wireless) between participating nodes. Nodes of the same subtree are physically connected. The identifier of a subtree is the minimal (e.g. alphanumerical) identifier of all nodes that have addresses from that subtree. Dotted leaves illustrate currently unused addresses.<br clear="all" /> |
||
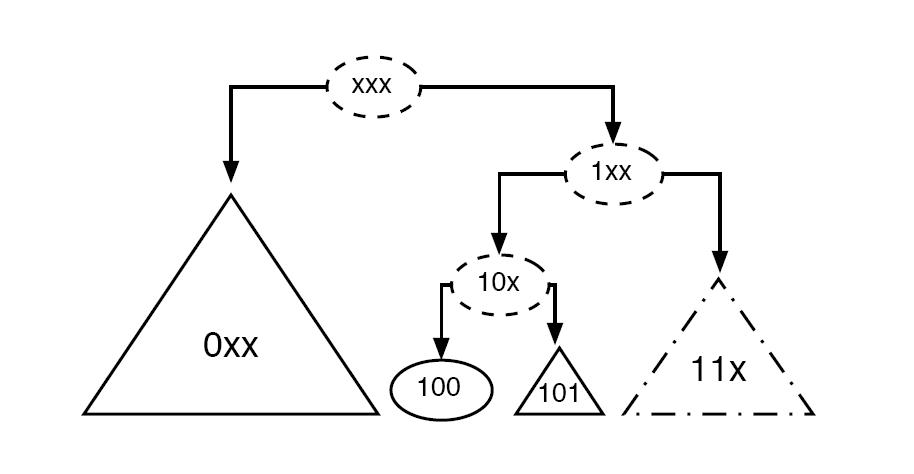
| ⚫ | [[Image:NetworkTopology.JPG|thumb|250px|A network topology]] The ''Network Topology'' view represents the connectivity between nodes. A crucial constraint ('''Prefix Subgraph Constraint''') is that all nodes that share a given address prefix form a connected subgraph in the network topology. This implies a coherence between address prefix length and distance between nodes. The longer the address prefix of a subgraph in the address tree, the shorter the expected distance between the nodes that share this prefix.<br clear="all" /> |
||
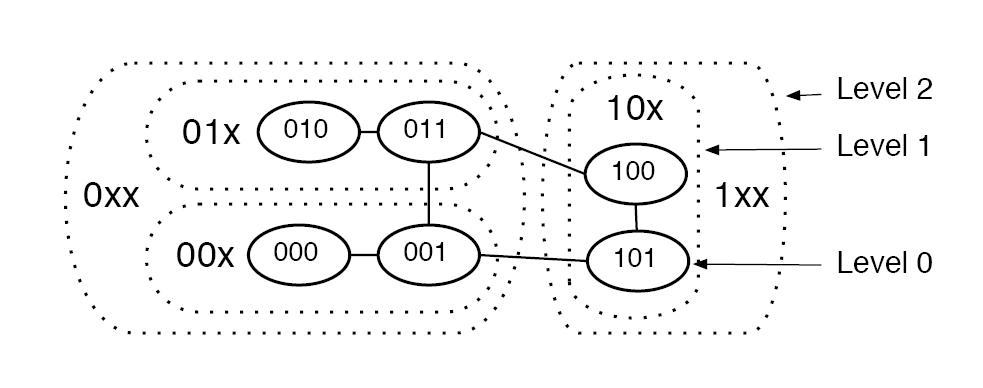
| ⚫ | [[Image:SiblingView.JPG|thumb|250px|The sibling view of the network]] Another important abstract view on the address space is the ''Sibling view''. A address tree of a ''l''-bit address consists of 2 Level-''(l-1)''-subtrees, 4 Level-''(l-2)''-subtrees and so on. Leaves are Level-''0''-subtrees. Each ''l''-bit address has ''l'' Level-''k''-siblings. In the example network the node with address 100 has one Level-''0''-sibling with the address (prefix) 101 (this sibling is only represented by the node with the same address 101), a Level-''1''-sibling with the address prefix 11x and Level-''2''-sibling (0xx).<br clear="all" /> |
||
| ⚫ | |||
| ⚫ | [[Image:NetworkTopology.JPG|thumb| |
||
[[Image:DARTRoutingTable.JPG|thumb|right|250px|Routing Table of node with address '100' in the example network]] Here a form of proactive distance vector routing is used, but other routing methods (e.g. link-state Routing) could also profit from dynamic addressing. A node's routing table consists of an entry for each Level-''k''-sibling of that node. If a node wants to send a packet to a peer whose address shares the same prefix with its own address, the packet is send to the representative of the Level-''((addressLength - 1) - prefixLength)''-sibling. For example, node 100 wants to route a packet to node 101. Because it shares a 2-bit address prefix with that peer, node 100 sends the packet to his Level-''0''-sibling's representative (in this case node 101 himself). The Prefix Subgraph Constraint guarantees that the Level-''k''-sibling's representative has a connection to the destined peer because of sharing the same address prefix. The procedure is repeated by the receiving node until the packet has reached its destination. |
|||
Assuming a balanced address tree, on average a routing table consists of O(log''n'') entries (n = number of nodes). A peer propagates its routing entries to its neighbors by periodic updates. |
|||
= Node Lookup = |
|||
An important question is how to find a node's current address. One promising approach is to use a distributed node lookup table shared by all nodes to store the ''<identifier, address>'' pairs. A node that stores the address of node Y is called Y's anchor node. A globally, a priori known hash function ''h(x)'' calculates the address of the anchor node for the peer with identifier ''x''. According to this hash function ''h(x)'' new nodes propagate their addresses to their anchor nodes, which in turn propagate them to requesting peers. |
|||
If the address returned by ''h(x)'' is unoccupied, then the address with the least edit distance is chosen and its corresponding peer becomes the anchor node. |
|||
= Dynamic Address Allocation = |
|||
When a node joins the network, it needs to gain a legitimate address. Listening to the periodic routing updates of its neighbors, the new node looks for the neighbor with the largest unoccupied address block and picks an address from that block. Obviously the ''Prefix Subgraph Constraint'' is satisfied. But what happens, if to mutual invisible nodes join the network and pick out address with the same prefix? In that case, the ''Prefix Subgraph Constraint'' is violated. Through periodic routing updates their adresses are propagated into the network. The first node that receives the conflicting information to that address subtree, compares the identifiers of the subtrees and drops the subtree with the higher ID. Listening to its neighbors updates the node with the invalid address learns about the conflict and chooses a new address. |
|||
Large address space is used to prevent refusing new node's request because of address congestion. Furthermore, address tree balancing is a technique to migrate nodes from highly congested adress spaces to less one without violating the ''Prefix Subgraph Constraint''. Eventually high degree of congestion can lead to address space expansion. |
|||
= Quellen = |
|||
| ⚫ | [[Image:SiblingView.JPG|thumb| |
||
* DART: Dynamic Address RouTing for Scalable Ad Hoc and Mesh Networks (by ''Eriksson'', ''Faloutsos'', ''Krishnamurthy'') |
|||
* PeerNet: Pushing Peer-To-Peer Down the Stack (by ''Eriksson'', ''Faloutsos'', ''Krishnamurthy'') |
|||
| ⚫ | |||
= Links = |
|||
[http://dart.cs.ucr.edu The DART Project] |
|||
Latest revision as of 08:24, 9 October 2007
The DART-Project was created by Jakob Eriksson, Michalis Faloutsos and Srikanth Krishnamurthy from the University of California, Riverside. Its former name was PeerNet.
Motivation
How large can an ad-hoc network be? Current ad hoc routing architectures do not scale well and work inefficiently in networks of more than a few hundred nodes. Those routing protocols use static addressing which leads to a massive overhead problem in mobile networks as the number of nodes grows. The main idea behind DART is to seperate node's address and identity. DART satisfies the following properties which can be seen as guideline for a scalable and efficient solution:
- Localization of overhead
- Lightweight, decentralized protocols
- Zero-configuration
- Minimal restrictions on hardware
Using dynamic addressing and appropriate routing, DART is a promising approach for achieving scalable routing in large ad hoc networks.
Principles
Identity & Address
The identity of a peer is a static number which is globally unique and stays the same throughout the lifetime of the node. The address of a node is represented by a k-bit number. It is dynamic and changes with node movement. Moreover, the address has a topological meaning since its current value reflects the node's location. The "address-disparate-identity" paradigma is totally opposed to traditional network protocols as IP.
Address space
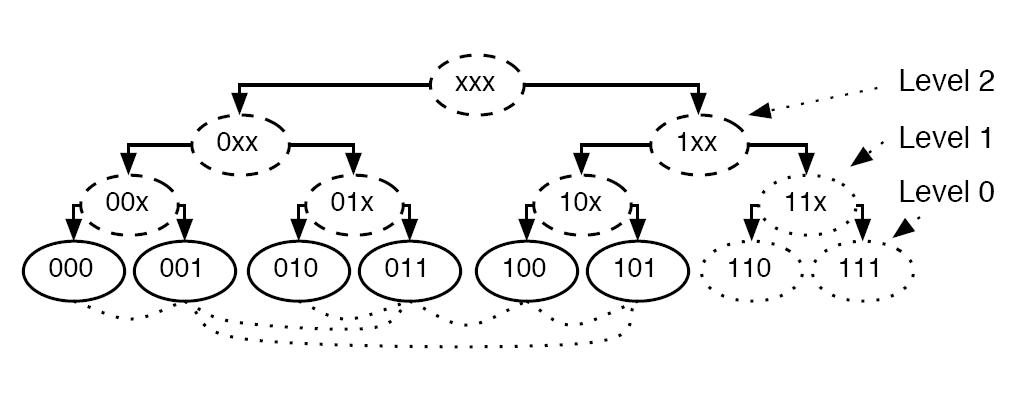
The Address Tree is an abstract visualization from the address space point of view. Its leaves represent peers in a network by their addresses. Its inner nodes represent address subtrees. An address subtree consists of nodes with the same address prefix. The dotted lines in the example image indicate physical links (wired or wireless) between participating nodes. Nodes of the same subtree are physically connected. The identifier of a subtree is the minimal (e.g. alphanumerical) identifier of all nodes that have addresses from that subtree. Dotted leaves illustrate currently unused addresses.
The Network Topology view represents the connectivity between nodes. A crucial constraint (Prefix Subgraph Constraint) is that all nodes that share a given address prefix form a connected subgraph in the network topology. This implies a coherence between address prefix length and distance between nodes. The longer the address prefix of a subgraph in the address tree, the shorter the expected distance between the nodes that share this prefix.
Another important abstract view on the address space is the Sibling view. A address tree of a l-bit address consists of 2 Level-(l-1)-subtrees, 4 Level-(l-2)-subtrees and so on. Leaves are Level-0-subtrees. Each l-bit address has l Level-k-siblings. In the example network the node with address 100 has one Level-0-sibling with the address (prefix) 101 (this sibling is only represented by the node with the same address 101), a Level-1-sibling with the address prefix 11x and Level-2-sibling (0xx).
Routing
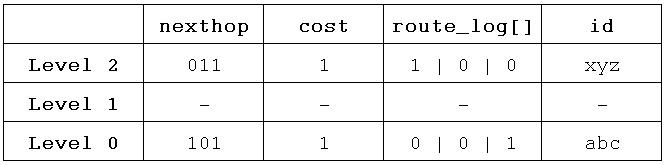
Here a form of proactive distance vector routing is used, but other routing methods (e.g. link-state Routing) could also profit from dynamic addressing. A node's routing table consists of an entry for each Level-k-sibling of that node. If a node wants to send a packet to a peer whose address shares the same prefix with its own address, the packet is send to the representative of the Level-((addressLength - 1) - prefixLength)-sibling. For example, node 100 wants to route a packet to node 101. Because it shares a 2-bit address prefix with that peer, node 100 sends the packet to his Level-0-sibling's representative (in this case node 101 himself). The Prefix Subgraph Constraint guarantees that the Level-k-sibling's representative has a connection to the destined peer because of sharing the same address prefix. The procedure is repeated by the receiving node until the packet has reached its destination.
Assuming a balanced address tree, on average a routing table consists of O(logn) entries (n = number of nodes). A peer propagates its routing entries to its neighbors by periodic updates.
Node Lookup
An important question is how to find a node's current address. One promising approach is to use a distributed node lookup table shared by all nodes to store the <identifier, address> pairs. A node that stores the address of node Y is called Y's anchor node. A globally, a priori known hash function h(x) calculates the address of the anchor node for the peer with identifier x. According to this hash function h(x) new nodes propagate their addresses to their anchor nodes, which in turn propagate them to requesting peers. If the address returned by h(x) is unoccupied, then the address with the least edit distance is chosen and its corresponding peer becomes the anchor node.
Dynamic Address Allocation
When a node joins the network, it needs to gain a legitimate address. Listening to the periodic routing updates of its neighbors, the new node looks for the neighbor with the largest unoccupied address block and picks an address from that block. Obviously the Prefix Subgraph Constraint is satisfied. But what happens, if to mutual invisible nodes join the network and pick out address with the same prefix? In that case, the Prefix Subgraph Constraint is violated. Through periodic routing updates their adresses are propagated into the network. The first node that receives the conflicting information to that address subtree, compares the identifiers of the subtrees and drops the subtree with the higher ID. Listening to its neighbors updates the node with the invalid address learns about the conflict and chooses a new address. Large address space is used to prevent refusing new node's request because of address congestion. Furthermore, address tree balancing is a technique to migrate nodes from highly congested adress spaces to less one without violating the Prefix Subgraph Constraint. Eventually high degree of congestion can lead to address space expansion.
Quellen
- DART: Dynamic Address RouTing for Scalable Ad Hoc and Mesh Networks (by Eriksson, Faloutsos, Krishnamurthy)
- PeerNet: Pushing Peer-To-Peer Down the Stack (by Eriksson, Faloutsos, Krishnamurthy)